040. Уравнения высших степеней
Уравнение вида ![]()
![]() – это Алгебраическое уравнение степени
– это Алгебраическое уравнение степени ![]() .
.
Если ![]() , то уравнение называется уравнением высшей степени. Например,
, то уравнение называется уравнением высшей степени. Например, ![]() – это уравнение третьей
– это уравнение третьей
степени.
Алгебраическое уравнение степени ![]() имеет не более
имеет не более ![]() действительных корней.
действительных корней.
Если ![]() тогда для уравнения
тогда для уравнения ![]() справедлива теорема Безу.
справедлива теорема Безу.
Теорема Безу. Многочлен ![]() делится без остатка на двучлен
делится без остатка на двучлен ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() – это корень многочлена
– это корень многочлена ![]() .
.
Например, многочлен ![]() делится без остатка на двучлен
делится без остатка на двучлен ![]() т. к.
т. к. ![]() – это корень уравнения
– это корень уравнения ![]() .
.
Если ![]() – многочлен с целыми коэффициентами, то любой целый корень многочлена
– многочлен с целыми коэффициентами, то любой целый корень многочлена ![]() является делителем свободного члена
является делителем свободного члена ![]() .
.
Например, ![]() – многочлен второй степени; его корни
– многочлен второй степени; его корни ![]() и
и ![]() – это делители свободного члена (числа 12).
– это делители свободного члена (числа 12).
Если существует хотя бы один целый корень уравнения, то Уравнения высших степеней решают так:
1) находят множество делителей свободного члена ![]() ;
;
2) проверяют, какие из этих делителей являются корнями уравнения ![]() (используя теорему Безу);
(используя теорему Безу);
3) находят частное от деления ![]() на
на ![]() , где
, где ![]() – корень уравнения
– корень уравнения ![]() ;
;
4) записывают  как многочлен степени
как многочлен степени ![]() :
: 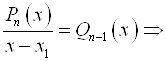
![]() , где
, где ![]() – многочлен степени
– многочлен степени ![]() ;
;
5) проверяют, являются ли корни многочлена ![]() также и корнями исходного уравнения.
также и корнями исходного уравнения.
Пример 18. Решите уравнение ![]() .
.
Решение. 1) Находим множество делителей свободного члена: это ![]() .
.
2) Проверяем, какой из делителей является корнем заданного уравнения.
При ![]() , получим:
, получим: ![]()
![]()
![]() – это корень заданного уравнения.
– это корень заданного уравнения.
При ![]() , получим:
, получим: ![]()
![]()
![]() – это не корень заданного уравнения.
– это не корень заданного уравнения.
3) Находим частное от деления многочлена ![]() на
на ![]() .
.
Получаем  .
.
4) Записываем частное как многочлен степени ![]() :
:
![]()
![]()

![]()

Ответ. 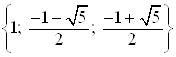 .
.
Пример 19. Решите уравнение ![]() .
.
Решение. 1) Записываем делители свободного члена: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;![]() ;
;![]() ;
; ![]() ;
; ![]() . Подбором находим целый корень уравнения.
. Подбором находим целый корень уравнения.
2) Подставляем найденные делители в исходное уравнение.
При ![]() , получим:
, получим: ![]()
![]()
![]() – не является корнем заданного уравнения.
– не является корнем заданного уравнения.
При ![]() , получим:
, получим: ![]()
![]()
![]() – не является корнем заданного уравнения.
– не является корнем заданного уравнения.
При ![]() , получим:
, получим: ![]()
![]()
![]() – является корнем заданного уравнения.
– является корнем заданного уравнения.
3) По теореме Безу многочлен ![]() делится без остатка на
делится без остатка на ![]() . Выполним деление "углом":
. Выполним деление "углом":
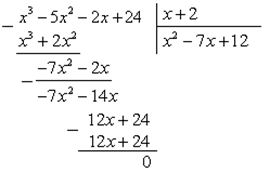
Представим многочлен в виде произведения двух сомножителей: ![]() .
.
![]()
![]()
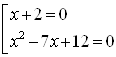
![]()
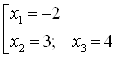
Ответ. ![]() .
.
Пример 20. Решите уравнение ![]() .
.
Решение. 1) Множество делителей свободного члена 1 – это ![]() . Но
. Но ![]() не являются корнями исходного уравнения.
не являются корнями исходного уравнения.
2) Найдем рациональные корни уравнения в виде ![]() , где
, где ![]() – делитель числа 1;
– делитель числа 1; ![]() – делитель числа 2 (2 – это старший коэффициент уравнения).
– делитель числа 2 (2 – это старший коэффициент уравнения). ![]() и
и ![]() – это взаимно простые числа. Такими корнями могут быть:
– это взаимно простые числа. Такими корнями могут быть: ![]() .
.
3) Проверим ![]() . После подстановки, находим корень уравнения
. После подстановки, находим корень уравнения ![]() .
.
4) Разделим многочлен на 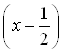 или
или 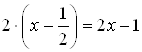 , чтобы при делении не было дробных коэффициентов.
, чтобы при делении не было дробных коэффициентов.
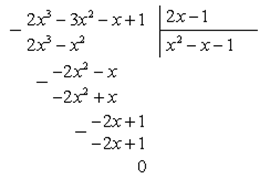
5) Получаем: ![]() .
.
![]()
![]()

![]()

Ответ.  .
.
Если корень уравнения ![]() – это дробь
– это дробь ![]() , тогда
, тогда ![]() – это делитель старшего коэффициента
– это делитель старшего коэффициента ![]() , а
, а ![]() – это делитель свободного члена
– это делитель свободного члена ![]() .
.
| < Предыдущая | Следующая > |
|---|