039. Трехчленные уравнения. Биквадратные уравнения

Уравнение вида называется Трехчленным, если , , , , .

Если , то уравнение называется Биквадратным уравнением.

Заменой переменной трехчленное уравнение преобразуется в квадратное .

Пример 15. Решите уравнение .

Решение. Пусть , тогда ; ;

; .

Ответ. .

Пример 16. Решите уравнение .

Решение. Пусть , тогда ; .

Если , то . Разложим это выражение на множители, используя формулу суммы кубов:

.

Приравняем выражения в скобках к нулю и найдем корни уравнения:

А)  ;

Б)  –уравнение не имеет действительных корней, т. к. .

Если , то . Тогда,

.

Приравняем выражения в скобках к нулю и найдем корни уравнения:

А)  ;

Б)  – это уравнение не имеет действительных корней, потому что .

Ответ. Уравнение имеет два действительных корня: .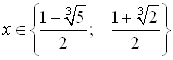

Пример 17. Решите уравнение .

Решение. Пусть , тогда , получим

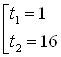
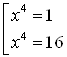
Ответ. .

< Предыдущая		Следующая >