044. Иррациональные уравнения

Иррациональные уравнения – это уравнения, в которых переменная стоит под знаком корня.

Например, – это иррациональные уравнения.

Основные методы решения иррациональных уравнений:

1) метод возведения обеих частей уравнения в одну и ту же степень;

2) метод введения новых переменных.

При решении иррациональных уравнений нужно делать проверку найденных корней или находить область допустимых значений уравнения.

Пример 32. Решите уравнение .

Решение. Находим ОДЗ уравнения: .

Ответ. Æ.

Пример 33. Решите уравнение .

Решение. Возведем в квадрат обе части уравнения, получим: . Выполним проверку.

Проверка. При – это корень данного уравнения.

Ответ. .

Пример 34. Решите уравнение .

Решение. Решим уравнение двумя способами.

I способ (с проверкой корней).

Возведем обе части уравнения в квадрат, получим:

Проверка. При , получим: значит – это корень уравнения.

При , получим: , значит – это не корень уравнения.

Ответ. .

II способ (с помощью эквивалентных преобразований).

Ответ. .

Пример 35. Решите уравнение .

Решение. Найдем ОДЗ: .

Возведем обе части уравнения в куб, используя формулу:

.

Тогда: ;

.

Возведем обе части уравнения в куб еще раз, получим:

Сделаем проверку:

А) Если , то ; – это корень уравнения.

Б) Если , то ; – это корень уравнения.

Ответ. .

Пример 36. Решите уравнение .

Решение. Найдем ОДЗ: . Возведем обе части уравнения в куб:

По условию: , тогда получим:

.

Разделим обе части уравнения на 3 и возведем их в куб:

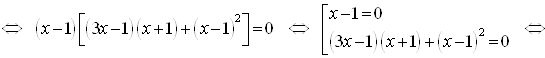
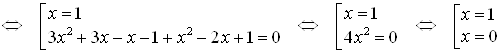
Сделаем проверку.

А) При , получим: – это корень уравнения.

Б) При , получим: – это не корень уравнения.

Ответ. .

Пример 37. Решите уравнение .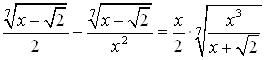

Решение. Вынесем общий множитель за скобки в левой части уравнения; приведем к общему знаменателю и сократим на 2, получим:

.

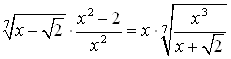Умножим правую и левую часть уравнения на , получим:

.

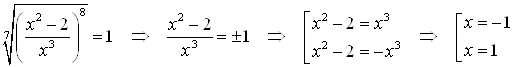Сделаем проверку.

При , получим:

Так же проверяем и убеждаемся, что это корень данного уравнения.

Ответ. .

Пример 38. Решите уравнение .

Решение. Сделаем замену переменной: . Тогда .

Получим:

Значит,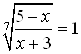

.

Проверка. Если тогда – это корень уравнения.

Ответ. .

Пример 39. Решите уравнение .

Решение. Сделаем преобразования:

; .

Сделаем замену переменной: , получим . Тогда, данное уравнение запишем так:

. Так как , то – это не корень уравнения.

Если то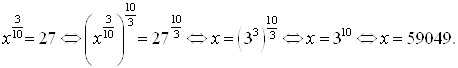

Проверка. Так как исходное уравнение эквивалентно уравнению то подставляя в это уравнение получим: – это корень исходного уравнения.

Ответ. .

< Предыдущая		Следующая >