037. Теорема Виета

Теорема Виета. Если и – корни квадратного уравнения , тогда их сумма равна , а произведение равно .

;

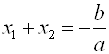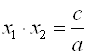
Докажем теорему Виета.

Дано: ; . .

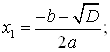
Доказать: .

Доказательство: ;

Из теоремы Виета следует, что квадратный трехчлен можно разложить на линейные множители:

Так, если , то .

Пример 13. Разложите квадратный трехчлен на линейные множители.

Решение. Найдем корни трехчлена. Для этого решим уравнение Þ ; ; .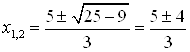

Так, .

Ответ. .

Теорема Виета для приведенного квадратного уравнения . Если приведенное квадратное уравнение имеет действительные корни и , то их сумма: , а произведение: .

Обратная теорема виета. Если сумма двух чисел и равна , а произведение этих чисел равно , то числа и – это корни уравнения .

Докажем обратную теорему Виета.

Дано: ; .

Доказать, что и – корни уравнения .

Доказательство: . Подставим в равенство получим: Þ Þ Следовательно, число – это корень уравнения .

Так же можно показать, что число – это тоже корень уравнения .

Используя обратную теорему Виета, можно составить квадратное уравнение по данным корням.

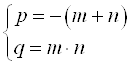Пусть ; . По теореме Виета: если , то .

Пример 14. Составьте квадратное уравнение с корнями ; .

Решение. По теореме Виета: ; .

Ответ. .

< Предыдущая		Следующая >