036. Линейные и квадратные уравнения
Уравнение вида ![]() называется Линейным Уравнением с одной переменной, где
называется Линейным Уравнением с одной переменной, где ![]() и
и ![]() – это заданные числа:
– это заданные числа: ![]() – это коэффициент при переменной
– это коэффициент при переменной ![]() ;
; ![]() – это свободный член.
– это свободный член.
Корень линейного уравнения: ![]() .
.
Пример 7. Решите уравнение: ![]() .
.
Решение. Сделаем эквивалентные преобразования:
![]() .
.
Ответ. ![]() .
.
Пример 8. Решите уравнение: ![]() .
.
Решение. Приведем дроби к общему знаменателю и сделаем эквивалент-ные преобразования: ![]()
![]()
![]()
![]()
Ответ. ![]() .
.
Уравнение вида ![]() (
(![]() ) называется Квадратным уравнением с одной переменной, где
) называется Квадратным уравнением с одной переменной, где ![]() – коэффициент при
– коэффициент при ![]() (первый коэффициент);
(первый коэффициент); ![]() – коэффициент при
– коэффициент при ![]() (второй коэффициент);
(второй коэффициент); ![]() – свободный член.
– свободный член.
Если ![]() , то квадратное уравнение называется Полным.
, то квадратное уравнение называется Полным.
Если ![]() или
или ![]() , то квадратное уравнение называется Неполным. Например,
, то квадратное уравнение называется Неполным. Например, ![]()
![]()
![]() – это неполные квадратные уравнения.
– это неполные квадратные уравнения.
Если ![]() , то квадратное уравнение называется Приведенным. Приведенное квадратное уравнение записывают так:
, то квадратное уравнение называется Приведенным. Приведенное квадратное уравнение записывают так: ![]() .
.
Корни квадратного уравнения ![]() находят по формуле:
находят по формуле: 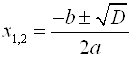 , где
, где ![]() – это дискриминант квадратного уравнения.
– это дискриминант квадратного уравнения.
Если второй коэффициент квадратного уравнения – это четное число, то корни такого квадратного уравнения можно находить по формуле: 
![]() .
.
1. Если ![]() , то уравнение
, то уравнение ![]() не имеет действительных корней.
не имеет действительных корней.
2. Если ![]() , то уравнение
, то уравнение ![]() имеет два равных корня:
имеет два равных корня:  .
.
3. Если ![]() , то уравнение
, то уравнение ![]() имеет два разных действительных корня.
имеет два разных действительных корня.
Пример 9. Решите уравнение: ![]() .
.
Решение. Имеем ![]() ;
; ![]() ;
; ![]() . Найдем дискриминант уравнения:
. Найдем дискриминант уравнения: ![]() , значит уравнение имеет два действительных корня. По формуле корней квадратного уравнения найдем эти корни:
, значит уравнение имеет два действительных корня. По формуле корней квадратного уравнения найдем эти корни:
 ; Þ
; Þ ![]() ;
; ![]() .
.
Ответ. ![]() ;
; ![]() .
.
Пример 10. Решите уравнение: ![]()
Решение. Найдем дискриминант уравнения: ![]() Þ уравнение не имеет действительных корней.
Þ уравнение не имеет действительных корней.
Ответ. Æ.
Пример 11. Решите уравнение: ![]() .
.
Решение. Найдем дискриминант уравнения: ![]() , следовательно
, следовательно ![]() . Уравнение имеет два равных корня.
. Уравнение имеет два равных корня.
Ответ. ![]() .
.
Пример 12. Решите уравнение: ![]() .
.
Решение. Используем формулу корней квадратного уравнения, когда коэффициент при ![]() – четное число.
– четное число.
Имеем ![]() ;
; ![]() ;
; ![]() .
.
Тогда 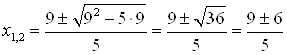 ;
; ![]() ;
; ![]() .
.
Ответ. ![]() ;
; ![]() .
.
| < Предыдущая | Следующая > |
|---|