035. Равенства. Тождества. Уравнения

Равенство – это два выражения, между которыми стоит знак "=" (равно). Например, – это равенство, где – это левая часть равенства, – это правая часть равенства.

Свойства равенств:

1) ; 2) ;

3) ; 4) ;

5) .

Равенства бывают: Числовые или С переменными.

Числовое равенство может быть Верным или Неверным.

Например, 1) ; – это верные числовые равенства; ; – это неверные числовые равенства.

2) – это равенство с переменными. Переменные и в этом равенстве могут принимать различные числовые значения. Если а , то – это верное числовое равенство. Если а , то – это неверное числовое равенство.

Тождество – это равенство с переменными, которое будет верным числовым равенством при любых значениях переменных.

Например, ; ; , если ; 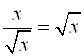, если – это тождества.

Уравнение – это равенство с переменными, которое будет верным числовым равенством при определенных значениях переменных.

Так, – это уравнение с одной переменной ,
Где и – это алгебраические выражения; – это переменная или неизвестная.

Например, – это уравнение с одной перемен-ной ; – это уравнение с двумя переменными и .

Корень (решение) уравнения – это такое значение переменной, при котором уравнение будет верным числовым равенством.

Решить уравнение – это значит найти все его корни или доказать, что их нет.

Пример 1. Решите уравнение .

Решение. Выполним тождественные преобразования: . Это уравнение имеет один единственный корень . Только если уравнение будет верным числовым равенством: , или .

Ответ. .

Пример 2. Найдите корни уравнения .

Решение. .

– это множество корней уравнения.

Ответ. .

Пример 3. Найдите корни уравнения .

Решение. , следовательно, это уравнение не имеет действительных корней (не имеет решений в области действительных чисел).

Ответ. Æ.

Пример 4. Найдите решение уравнения .

Решение. Уравнение имеет бесчисленное множество корней (решений). Любое неотрицательное число – это решение данного уравнения.

Ответ. .

Область определения Уравнения (или область допустимых значений уравнения (ОДЗ или )) – это множество значений переменной , при которых имеют смысл (определены) левая и правая части уравнения.

Чтобы найти ОДЗ уравнения , нужно найти пересечение множеств, на которых определены заданные алгебраические выражения и .

Пример 5. Найдите область допустимых значений уравнения .

Решение. Найдем ОДЗ левой и правой части уравнения.

ОДЗ левой части уравнения – это все действительные числа, кроме :

ОДЗ правой части уравнения – это все положительные числа :

ОДЗ уравнения – это пересечение множеств и :

Ответ. .

Два уравнения и называются Равносильными (эквивалентными), если множества их корней (решений) совпадают: ( – это знак эквивалентности (равносильности)).

Например, 1) уравнения и – эквивалент-ны, т. к. эти уравнения имеют корень: ;

2) уравнения и не равносильны, т. к. уравнение имеет только один корень: , а уравнение имеет два корня: ; .

Рассмотрим некоторые эквивалентные преобразования, которые удобно использовать при решении уравнений.

Таблица 4.1 – Эквивалентные преобразования уравнений

№	Действия	Примеры
1.	Замена левой части уравнения на правую часть или правой части на левую
2.	Перенос слагаемых из одной части уравнения в другую с противоположным знаком
3.	Умножение или деление обеих частей уравнения на одно и то же число, не равное нулю
4.	Вычитание или прибавление одного и того же числа к обеим частям уравнения
5.	Вычитание или прибавление одного и того же алгебраического выражения к обеим частям уравнения. При этом области определения полученного и данного уравнения должны совпадать

В процессе решения уравнений при помощи эквивалентных преобразований, необходимо:

1) найти область допустимых значений (ОДЗ) исходного уравнения;

2) проверить, принадлежат ли полученные значения ОДЗ исходного уравнения.

Пример 6. Решите уравнение .

Решение. Найдем ОДЗ уравнения: . Преобразуем уравнение, для этого перенесем все члены уравнения в левую часть. Получим уравнение . Корни этого уравнения: ; . Но корень не принадлежит области допустимых значений (ОДЗ). Поэтому – это посторонний корень, который не нужно рассматривать. Решением уравнения будет .