028. Тождественные преобразования алгебраических дробей
Алгебраические дроби можно складывать, вычитать, умножать, делить, приводить к общему знаменателю, сокращать, возводить в степень, т. е. выполнять их Тождественные преобразования. Рассмотрим некоторые примеры.
I. Упростите выражения, используя основное свойство дроби (числитель и знаменатель дроби можно умножить или разделить на одно и то же число, отличное от нуля).
1. 
;
2. 
;
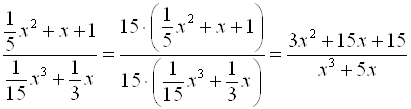3. 
; 
;
II. Сократите дроби.
1. 
;
2. 
;
3. 
;
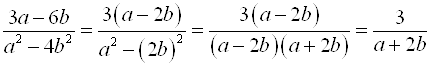4. 
.
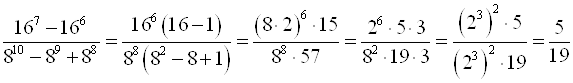III. Приведите дроби к общему знаменателю.
1.
; 
.
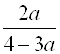Общий знаменатель данных дробей – это произведение знаменателей: 
.
;
.
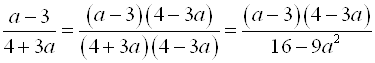2. 
; 
; 
.
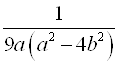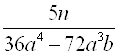Для того чтобы найти общий знаменатель, разложим знаменатели этих дробей на множители:
;
;
.
Наименьшее общее кратное чисел 
– это число 
. Поэтому общий знаменатель данных дробей – это: 
. Дополнительные множители для этих дробей: 
; 
; 
.
;
;
.
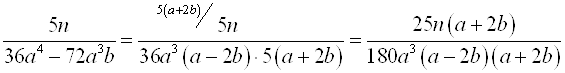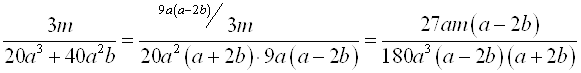3. 
; 
; 
.
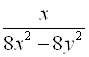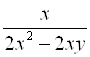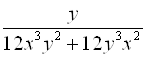Для того чтобы найти общий знаменатель, разложим знаменатели этих дробей на множители:
;
;
.
Общий знаменатель данных дробей – это: 
.
Дополнительные множители: 
; 
; 
.
;
;
.
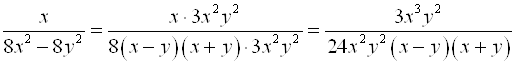IV. Выполните действия (сложение, вычитание, умножение и деление алгебраических дробей).
Для выполнения этих действий, нужно приводить алгебраические дроби к общему знаменателю и выполнять преобразования.
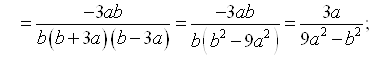
3. 
;
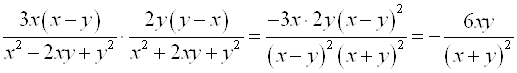4. 
;
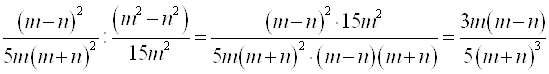5. 
.
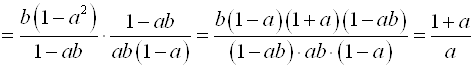V. Выполните тождественные преобразования.
1. 
.
Выполним сложение в скобках, для этого разложим на множители знаменатель первой дроби: 
. Знаменатель второй дроби запишем так: 
.
Получаем: 
– это общий знаменатель;
– это дополнительный множитель первой дроби;
– это дополнительный множитель второй дроби.
.
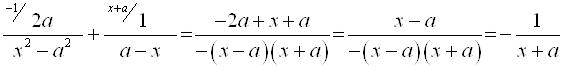Сократим на 
Дробь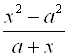 
, тогда получим:
.
Выполним умножение: 
.
Получим результат: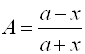 
.
2. 
.
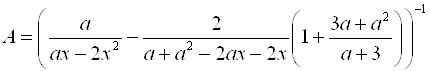Выполним преобразования:
.
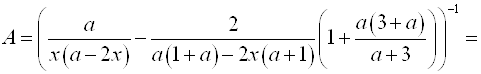
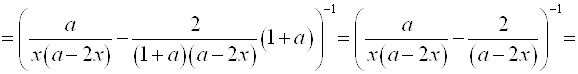
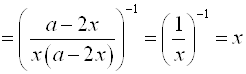Получим результат. 
.
3. 
.
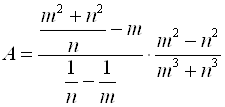Преобразуем числитель и знаменатель первой дроби:
; 
;
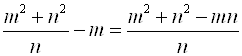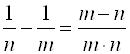Поэтому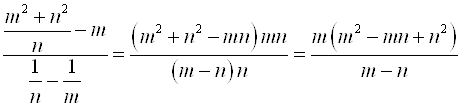 
.
Умножим первую дробь на вторую:
.
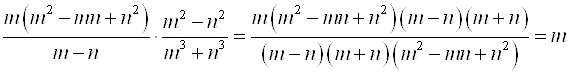Получим результат: 
.
4. 
.
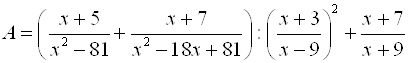Делаем действия последовательно. Сначала – сложение в первых скобках, для этого приводим дроби к общему знаменателю.
Разделим результат на вторую дробь.
.
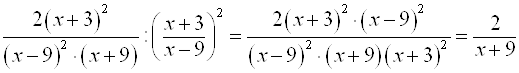Выполним сложение. 
.
Получим результат: 
.
5. 
.
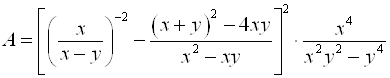Делаем действия последовательно.
1) 
;
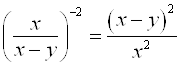2) 
;
3) 
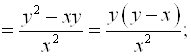
4) 
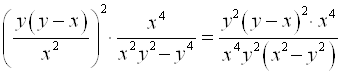; т. к. 
, после сокращения получаем: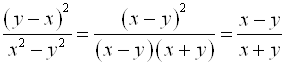 
.
Получим результат: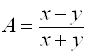 
.
| < Предыдущая | Следующая > |
|---|
