027. Теорема Безу. Использование теоремы Безу для разложения многочленов на множители

Пусть – это многочлен -й степени:

, .

Разделим на , получим: , где – это частное от деления на ; – остаток. Степень переменной остатка всегда меньше степени переменной делителя.

Пример 6. Разделите на .

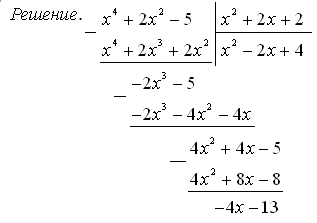
Значит, , где – это целая часть многочлена; – это остаток.

Ответ. .

Теорема Безу. Остаток от деления многочлена на равен .

Пример 7. Найдите остаток от деления .

Решение. Подставим в многочлен :

; .

Ответ. .

Следствия теоремы Безу.

1. Если многочлен делится на без остатка, то – это корень многочлена.

2. Если – это корень многочлена , то многочлен делится на без остатка.

Пример 8. При каком значении "" остаток от деления многочлена на равен нулю?

Решение.

.

Ответ. Остаток от деления равен нулю, если .

3. Если – многочлен с целыми коэффициентами, то любой целый корень многочлена является делителем его свободного члена .

Пример 9. Разложите на множители многочлен .

Решение. Найдем делители свободного члена – это числа 1 и 3.

При значениях и многочлен обращается в ноль, поэтому и – это корни многочлена. Многочлен делится без остатка на и на .

Выполним деление многочлена на углом:

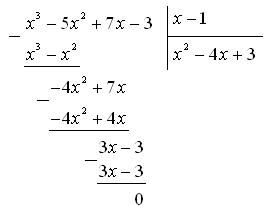
Получим:

Ответ. .

< Предыдущая		Следующая >