019. Действия с множествами

Чтобы описать операции над множествами, используем рисунки 2.3 – 2.6, которые называют диаграммами Эклера-Венне.

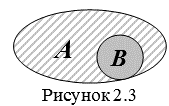
Множество называется Подмножеством множества , если каждый элемент множества является элементом множества . Записывают так: (рис. 2.3).

Например, а) множество натуральных чисел – это подмножество множества целых чисел . Записывают так: ;

Б) отрезок – это подмножество отрезка . Записывают так: ;

В) . Множество натуральных чисел () является подмножеством множества целых чисел (); множество является подмножеством множества рациональных чисел (); множество – подмножество множества действительных чисел ().

Объединение множеств и – это такое множество , которое состоит из всех элементов данных множеств. Записывают так: (рис. 2.4).

Например, а) множество действительных чисел – это объединение множества рациональных чисел и иррациональных чисел . Записывают так:

Б) если

То

В) .

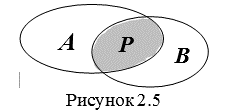
Пересечение множеств и – это такое множество , которое состоит из общих элементов данных множеств: (рис. 2.5).

Например, а) если , , то ;

Б) ;

В) если – это множество делителей числа 12, – это множество делителей числа 18, то множество – это множество общих делителей чисел 12 и 18;

Г) пересечение множества рациональных чисел и иррациональных чисел – это пустое множество: Æ.

Множество общих делителей чисел и – это пересечение множеств делителей данных чисел.

Разность множеств и – это такое множество которое состоит из всех элементов множества , таких, что не принадлежат множеству т. е. (рис. 2.6).

Например, если , , то .

< Предыдущая		Следующая >