018. Понятие множества

Понятие множества в математике не определяется. Например, множество студентов в группе, множество книг в библиотеке и так далее.

Множество представляют как совокупность объектов (предметов), которые объединены по общему признаку.

Множества состоят из элементов. Так, , , ... – это элементы множества .

Множества обозначают большими буквами латинского алфавита: , , и т. д.

Пишут так: . Читают так: "Множество состоит из элементов , , и так далее".

Если элемент принадлежит множеству , то записывают:

.

Пустое множество – это множество, у которого нет элементов. Пустое множество обозначают символом Æ.

Например, множеством решений неравенства будет Æ (пустое множество).

Множества бывают Конечные и Бесконечные. Например, – это конечное множество; – это бесконечное множество.

Множество четных чисел или множество нечетных чисел – это бесконечные множества.

Множества, элементами которых являются числа, называются Числовыми множествами. К таким множествам относятся:

1.  – Множество натуральных чисел.

Например, ; ; .

2.  – Множество целых чисел.

Например, ; ; .

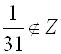Положительные числа – это числа со знаком "+". Отрицательные числа – это числа со знаком "-".

3. 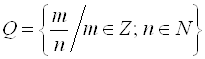 – Множество рациональных чисел.

Читаем эту запись так: "Множество состоит из элементов вида , таких что принадлежит множеству (целые числа), а принадлежит множеству (натуральные числа)".

Например, .

Целые числа, положительные и отрицательные числа, обыкновенные дроби, конечные десятичные дроби, бесконечные периодические дроби – это Рациональные числа.

4. Множество – Множество иррациональных чисел. Бесконечные непериодические дроби – это иррациональные числа.

Например, .

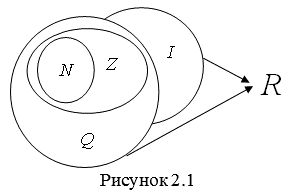
5. Множество – Множество действительных чисел. Все рациональные и иррациональные числа – это действительные числа (рис. 2.1).

Действительные числа можно показать точками на числовой оси (рис. 2.2).

Числовая ось (или Координатная прямая) – это прямая линия, на которой выбрано начало отсчета (точка "О"), единичный отрезок и направление.

Направление слева направо на координатной прямой называется положительным. А направление справа налево (т. е. противоположное) называется отрицательным.

Каждому действительному числу соответствует единственная точка числовой оси.

Если точка на числовой оси соответствует числу , то это число называют координатой точки и пишут: .

Например, точка изображает число 1; тогда 1 – это координата точки ; пишут так: точка изображает число , тогда – это координата точки: .

Возьмем два числа и , такие, что . Отметим на координатной прямой соответствующие им точки.

Любая точка , которая лежит между и , соответствует числу, которое удовлетворяет неравенству: .

Множество всех чисел, которые удовлетворяют неравенству , называется Открытым Интервалом или .

Множество всех чисел, которые удовлетворяют неравенству , называется Закрытым Интервалом или Отрезком .

или – это закрытый интервал, или отрезок;

или – это открытый интервал;

или , или – это полуинтервалы (полуоткрытый или полузакрытый интервалы).

Интервалы и отрезки – это конечные числовые Промежутки. Существуют и бесконечные числовые промежутки.

Множество всех чисел которые удовлетворяют неравенству , называются Числовым лучом: .

– это также числовой луч, если .

Числовые лучи – это бесконечные числовые промежутки.

Например, множество действительных чисел можно обозначать так: . Знак "" читают: "плюс бесконечность"; знак "" читают: "минус бесконечность".

Геометрически числовые промежутки можно представить так (табл. 2.1):

Таблица 2.1 – Числовые промежутки

< Предыдущая		Следующая >