014. Пропорции
Пропорция – это равенство двух отношений.
 или
или ![]() ; где
; где ![]() ;
; ![]() .
.
Здесь ![]() и
и ![]() – это Крайние члены пропорции;
– это Крайние члены пропорции; ![]() и
и ![]() – это Средние члены пропорции;
– это Средние члены пропорции; ![]() – это левая часть пропорции;
– это левая часть пропорции; ![]() – это правая часть пропорции.
– это правая часть пропорции.
Читаем пропорцию так: ![]() относится к
относится к ![]() , как
, как ![]() относится к
относится к ![]() .
.
Например, пропорция 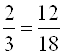 читается так: два относится к трем, как двенадцать относится к восемнадцати;
читается так: два относится к трем, как двенадцать относится к восемнадцати; 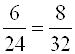 – шесть относится к двадцати четырем, как восемь относится к тридцати двум.
– шесть относится к двадцати четырем, как восемь относится к тридцати двум.
Основное свойство пропорции. Произведение крайних членов пропорции равно произведению средних членов пропорции:
Если  , то
, то ![]() , где
, где ![]() ,
, ![]() .
.
Например, для пропорции 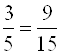 ; числа 3 и 15 – это крайние члены пропорции; а числа 5 и 9 – это средние члены пропорции. По основному свойству пропорции запишем:
; числа 3 и 15 – это крайние члены пропорции; а числа 5 и 9 – это средние члены пропорции. По основному свойству пропорции запишем:
![]() , т. е.
, т. е. ![]() .
.
Для пропорции  ;
; ![]() и
и ![]() – это крайние члены пропорции;
– это крайние члены пропорции; ![]() и
и ![]() – это средние члены пропорции, тогда
– это средние члены пропорции, тогда
 ;
; 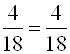 .
.
Чтобы найти неизвестный член пропорции, используем основное свойство пропорции.
Пример 15. Найдите неизвестный член пропорции 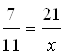 .
.
Решение. Используя основное свойство пропорции имеем: ![]() , откуда:
, откуда: 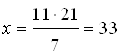
Ответ. ![]() .
.
Пример 16. Найдите ![]() из пропорции:
из пропорции: 
Решение. ![]() ;
;
![]() ;
;
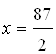 ;
;
![]() .
.
Ответ. ![]()
В пропорции ![]() можно переставлять:
можно переставлять:
1) средние члены: ![]() ;
;
2) крайние члены: ![]() ;
;
3) крайние члены ![]() и
и ![]() – на место средних членов
– на место средних членов ![]() и
и ![]() ; средние члены
; средние члены ![]() и
и ![]() – на место крайних членов
– на место крайних членов ![]() и
и ![]() , т. е.:
, т. е.: ![]() .
.
В каждой из полученных пропорций можно менять местами левую и правую части. Получим новые пропорции:
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Например, если дана пропорция: ![]() , то можно записать такие новые пропорции: 1)
, то можно записать такие новые пропорции: 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() 4)
4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() ; 7)
; 7) ![]() .
.
Если дана пропорция ![]() , то можно записать такие новые пропорции:
, то можно записать такие новые пропорции:
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4) 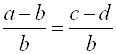 ; 5)
; 5)  ; 6)
; 6) 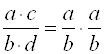 .
.
Например, если дана пропорция: 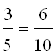 , то можно составить следующие новые пропорции:
, то можно составить следующие новые пропорции:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4) 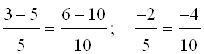 ;
;
5) 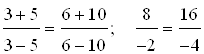 ; 6)
; 6) 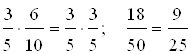 .
.
| < Предыдущая | Следующая > |
|---|