013. Отношения

Частное чисел и – это Отношение этих чисел, где .

Отношение можно записать в виде: или , где и – это члены отношения.

Читаем отношение так: "отношение к Равно ".

Например, отношение читаем так: "отношение четырех к двум равно двум".

Таблица 1.15 – Отношения

Число	Отношение
Чего? (родительный падеж)	К чему? (дательный падеж)
1	Одного	Одному
2	Двух	Двум
3	Трех	Трем
4	Четырех	Четырем
5	Пяти	Пяти
6	Шести	Шести
...	...	...
20	Двадцати	Двадцати
...	...	...
40	Сорока	Сорока
...	...	...

Если , то отношение показывает, во сколько раз больше, чем . Например, (отношение пятнадцати к трем равно пяти). Это отношение показывает, что 15 в 5 раз больше, чем 3.

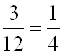Если , то отношение показывает, какую часть составляет от . Например, (отношение трех к двенадцати равно дроби "одна четвертая"). Это отношение показывает, что число 3 составляет часть от числа 12.

Если , то числа и равны. Например, (отношение семи к семи равно единице (одному). Это отношение показывает, что числа равны между собой.

Свойство отношения. Отношение не изменится, если члены отношения умножить или разделить на одинаковое число (это число не равно нулю).

, где , .

Следовательно,

А) отношения можно сокращать;

Б) отношение дробей можно записать как отношение целых
чисел.

Пример 14. Запишите отношение дробей как отношение целых чисел.

Решение. Найдем наименьший общий знаменатель: НОЗ=15. Умножим члены отношения на 15, получим:

.

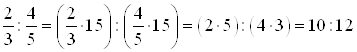Ответ. .

< Предыдущая		Следующая >