49. Человек бродит по городу

На рис. 11 изображен план города (столь правильный вид имеет, например, план Канберры — столицы Австралии). В этом гороДЕ прямоугольных кварталов, разделенныХ «горизонтальными» и «ВерТИкальными» улицами. Путник хочет попастЬ из пункта А В Пункт В кратчайшим путем, т. Е. двигаясь все время или «слева Направо», или «Снизу вверх». Сколькими путями он может добратЬСя из А в B?

Ясно, что, каким бы путем НИ шел путник, он пройдеТ Через перекрестков (считая точку А, но не Считая Точки В). На каждом перекрестке он может идти Или Направо, или вверх. В соответствии с этим все перекрестКи делятся на два класса: «перекрестки направо» и «перЕКрестки вверх». При ЭТом направо путник идет K раз, а вверх П раз. Значит, чтобы однозначно восстановить его путь, надо знать лишь те K случаев, когда он идет направо. Но их можно выбрать из общего числа П + K перекрестков способами. Поэтому число искомых путей равно .

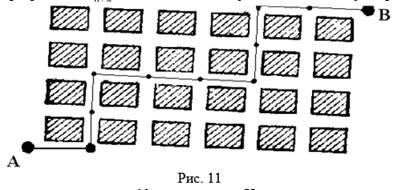
На рис. 11 изображен путь, проходящий через 10 перекрестков. Направо путник идет на перекрестках с НОмерами 1, 4, 5, 6, 9 и 10.

Решим теперь ЗАдачу, предлагавшуюся в 1945 г. на VIII Московской математической олимпиадЕ.

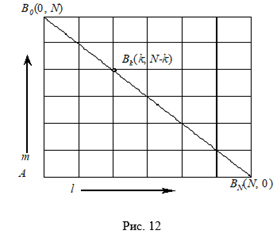
Имеется сеть дорог (рис. 12). Из пункта А выходят человек. Половина из них идет по направлению L, а Половина — по направлению т. Дойдя до первого перекрестКа, каждая группа разделяется: половина идет пО напраВлЕнию l, а половина — по направлению т. Такое же Разделение прОИсходит на каждом перекресткЕ. В каких пунктах окажутся ЭТи люди после того, каК они проЙДУТ N перекрестков И сколько людей будет в каждом из Этих пунктов?

Так как общее число пройденных каждым человеком отрезков пути равно N, то люди окажутся в пунКТах , Имеющих координаты вида , где K принимаеТ значения от 0 до N. Все эти пункты расположены на прямой (см. рис. 12), где .

Теперь остается узнать, сколько человек придет в пуНКт . Из точки А в каждый пункт , Ведут путей, причем .

Значит, число путей, идущих из пункта А В пункты, расположенные на прямой , равно , Т. е. в тОЧности равно числу людей, вышедшиХ из пункта А. Это Означает, что каждый путь пройдет один и только один человек, а количеСТво людей, оказавшихся в пункте , равно числу путей из А в , т. е. . Если в каждом пункте указать количество пришедших туда людей, то по линии окажутся выписанными числа -Й строки арифметического треугольника.

< Предыдущая		Следующая >