48. Арифметический треугольник

Формула (10) дает простой способ последовательного вычисления значений . Сначала надо написать значение . В следующей строке НАпишем значения И так, чтобы значение оказалось над Промежутком между этими двумя числами. Далее, мы знаем, что . Эти числа запишем в следующей строкЕ. А между ними запишем число . Но по формуле (10) Значит, равно сумме чИСел предыдущеЙ строки, стоящих слева и справа от него, По тому же правилу заполняем остальные строки: сначала пишем по бокам значения , а всЕ промежуточные значения вычисляем как суммы чисел предыдуЩЕй строки, стоящих слева и справа от вычисляемого зНАчения. В результате получаем такой числовой треугольник:

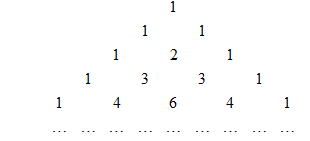
Его называют Арифметическим треуголЬНиком.

При составлении арифметического треугольника каждое число N-й строки участвует в образовании двух чисел -й строки — стоящего слева и стоящего справа от него. Поэтому если сложить числа -й строки ЧЕрез одно, то в полученную сумму войдут по одному разу все числа N-й строки. Складывать числа через одно МОжно двумя способами, — начав с первого числа строки или начав со второго числа. В обоих случаях получится одна и та же сумма, равная сумме чисел в N-й строке.

Доказанное свойство арифметического треугольника можно ЗАписать так;

(11)

Из него следует, что сумма чисел -й строки вдвое больше суммы чисел N-й строки. Иными словами, при переходе к следующей строке арифметического ТреугольНика сумма чисел в строке удваивается. Но в первой строке стоит только одно число 1, а потому для нее сумма равна 1. Поэтому в -й строке сумма чисел равна

(12)

< Предыдущая		Следующая >