12. Варианты контрольной работы № 2
1. Найти частные производные ![]() функции
функции ![]() .
.
1.1. ![]() 1.2.
1.2. ![]()
1.3. 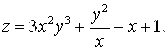 1.4.
1.4. 
1.5. ![]() 1.6.
1.6. ![]()
1.7.  1.8.
1.8. 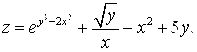
1.9. ![]() 1.10.
1.10. ![]()
1.11. 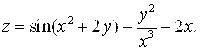 1.12.
1.12. 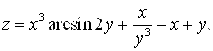
1.13. ![]() 1.14.
1.14. ![]()
1.15. ![]() 1.16.
1.16. ![]()
1.17. 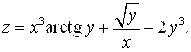 1.18.
1.18. ![]()
1.19. ![]() 1.20.
1.20. ![]()
2. Найти экстремумы функции ![]() .
.
2.1. ![]() 2.2.
2.2. ![]()
2.3. ![]() 2.4.
2.4. ![]()
2.5. ![]() 2.6.
2.6. ![]()
2.7.![]() 2.8.
2.8. ![]()
2.9. ![]() 2.10.
2.10. ![]()
2.11. ![]() 2.12.
2.12. ![]()
2.13. ![]() 2.14.
2.14. ![]()
2.15. ![]() 2.16.
2.16. ![]()
2.17. ![]() 2.18.
2.18. ![]()
2.19. ![]() 2.20.
2.20. ![]()
3. Вычислить двойной интеграл по области D, ограниченной указанными линиями, (сделать чертеж).
3.1. ![]() 3.2.
3.2. ![]()
3.3. ![]() 3.4.
3.4. ![]()
3.5. ![]() 3.6.
3.6. ![]()
3.7. ![]()
3.8.![]()
3.9. ![]()
3.10. ![]()
3.11. ![]()
3.12. ![]()
3.13. ![]()
3.14. ![]()
3.15. ![]()
3.16. ![]()
3.17. ![]()
3.18. ![]()
3.19. ![]()
3.20. ![]()
4. Вычислите криволинейный интеграл.
 ,
,
где ![]() – дуга параболы
– дуга параболы ![]() от точки А(0;0) до точки В(1;1).
от точки А(0;0) до точки В(1;1).
 ,
,
где ![]() – дуга параболы
– дуга параболы ![]() от точки А(0;0) до точки В(1;2).
от точки А(0;0) до точки В(1;2).
 ,
,
где ![]() – дуга параболы
– дуга параболы ![]() от точки А(0;0) до точки В(1;1).
от точки А(0;0) до точки В(1;1).
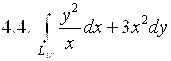 ,
,
где ![]() – дуга линии
– дуга линии ![]() от точки А(1;0) до точки В(E;1).
от точки А(1;0) до точки В(E;1).
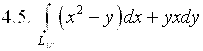 ,
,
где ![]() – дуга параболы
– дуга параболы ![]() от точки А(0;0) до точки В(1;2).
от точки А(0;0) до точки В(1;2).
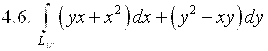 ,
,
где ![]() – дуга параболы
– дуга параболы ![]() от точки А(0;0) до точки В(2;2).
от точки А(0;0) до точки В(2;2).
 ,
,
где ![]() – дуга параболы
– дуга параболы ![]() от точки А(0;0) до точки В(3;3).
от точки А(0;0) до точки В(3;3).
 ,
,
где ![]() – дуга параболы
– дуга параболы ![]() от точки А(0;0) до точки В(2;2).
от точки А(0;0) до точки В(2;2).
 ,
,
где ![]() – дуга параболы
– дуга параболы ![]() от точки А(0;0) до точки В(1;1).
от точки А(0;0) до точки В(1;1).
 ,
,
где ![]() – дуга параболы
– дуга параболы ![]() от точки А(0;0) до точки В(1;2).
от точки А(0;0) до точки В(1;2).
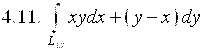 ,
,
где ![]() – дуга параболы
– дуга параболы ![]() от точки А(0;0) до точки В(1;1).
от точки А(0;0) до точки В(1;1).
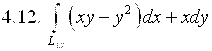 ,
,
где ![]() – дуга параболы
– дуга параболы ![]() от точки А(0;0) до точки В(1;1).
от точки А(0;0) до точки В(1;1).
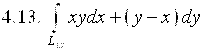 ,
,
где ![]() – дуга параболы
– дуга параболы ![]() от точки А(0;0) до точки В(1;1).
от точки А(0;0) до точки В(1;1).
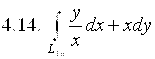 ,
,
где ![]() – дуга линии
– дуга линии ![]() от точки А(1;0) до точки В(E;1).
от точки А(1;0) до точки В(E;1).
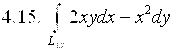 ,
,
где ![]() – дуга параболы
– дуга параболы  от точки А(0;0) до точки В(2;1).
от точки А(0;0) до точки В(2;1).
 ,
,
где ![]() – дуга параболы
– дуга параболы ![]() от точки А(-1;1) до точки В(1;1).
от точки А(-1;1) до точки В(1;1).
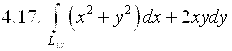 ,
,
где ![]() – дуга линии
– дуга линии ![]() от точки А(0;0) до точки В(1;1).
от точки А(0;0) до точки В(1;1).
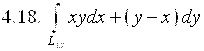 ,
,
где ![]() – дуга линии
– дуга линии ![]() от точки А(0;0) до точки В(1;1).
от точки А(0;0) до точки В(1;1).
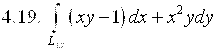 ,
,
где ![]() – дуга параболы
– дуга параболы ![]() от точки А(1;1) до точки В(3;-3).
от точки А(1;1) до точки В(3;-3).
 ,
,
где ![]() – дуга параболы
– дуга параболы ![]() от точки А(1;1) до точки В(2;4).
от точки А(1;1) до точки В(2;4).
5. Найти интервал и область сходимости степенного ряда:
5.1.  . 5.2.
. 5.2. 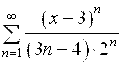 . 5.3.
. 5.3.  .
.
5.4.  . 5.5.
. 5.5. 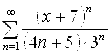 . 5.6.
. 5.6.  .
.
5.7.  . 5.8.
. 5.8. 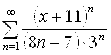 . 5.9.
. 5.9. 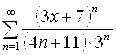 .
.
5.10.  . 5.11.
. 5.11.  . 5.12.
. 5.12.  .
.
5.13. 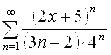 . 5.14.
. 5.14. 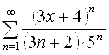 . 5.15.
. 5.15.  .
.
5.16. 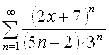 . 5.17.
. 5.17. 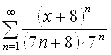 . 5.18.
. 5.18. 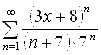 .
.
5.19.  . 5.20.
. 5.20.  .
.
6. Используя разложение подынтегральной функции в степенной ряд, вычислить указанный определенный интеграл с точностью до 0,01.
6.1. 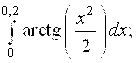 6.2.
6.2.  6.3.
6.3. 
6.4.  6.5.
6.5. 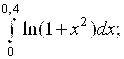 6.6.
6.6. 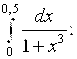
6.7. 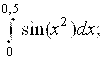 6.8.
6.8. 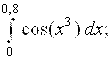 6.9.
6.9. 
6.10. 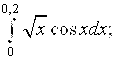 6.11.
6.11.  6.12.
6.12. 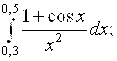
6.13. 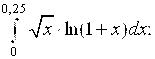 6.14.
6.14.  6.15.
6.15. 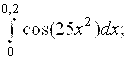
6.16. 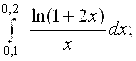 6.17.
6.17.  6.18.
6.18. 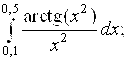
6.19. 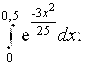 6.20.
6.20. 
7. Разложить в ряд Фурье функцию ![]() , заданную на отрезке
, заданную на отрезке ![]() .
.

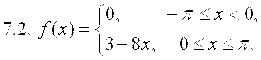
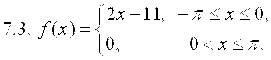


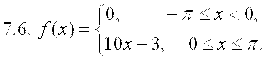
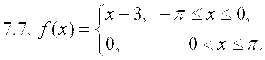
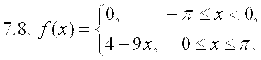
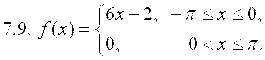
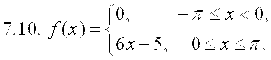
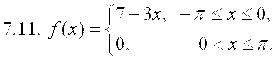
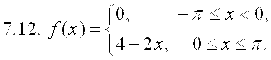
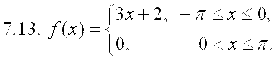
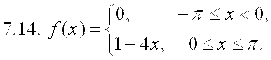
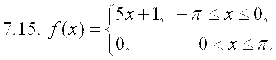
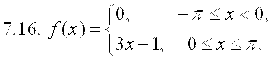
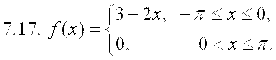
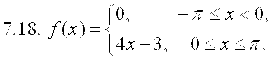
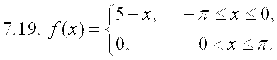
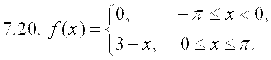
8. Вероятность изготовления детали высшего качества равна P. Найти вероятность того, что среди N наудачу взятых деталей будет от ![]() до
до ![]() деталей высшего качества. Вычисления производить с точностью до 0,001.
деталей высшего качества. Вычисления производить с точностью до 0,001.
|
№ |
8.1 |
8.2 |
8.3 |
8.4 |
8.5 |
8.6 |
8.7 |
8.8 |
8.9 |
8.10 |
|
P |
0,6 |
0,7 |
0,8 |
0,6 |
0,5 |
0,4 |
0,7 |
0,8 |
0,9 |
0,6 |
|
|
5 |
6 |
7 |
8 |
5 |
6 |
7 |
8 |
5 |
6 |
|
|
2 |
1 |
3 |
0 |
2 |
3 |
3 |
2 |
1 |
2 |
|
|
4 |
3 |
5 |
3 |
4 |
5 |
5 |
4 |
4 |
5 |
|
№ |
8.11 |
8.12 |
8.13 |
8.14 |
8.15 |
8.16 |
8.17 |
8.18 |
8.19 |
8.20 |
|
P |
0,4 |
0,6 |
0,7 |
0,8 |
0,6 |
0,5 |
0,7 |
0,9 |
0,4 |
0,8 |
|
|
7 |
8 |
5 |
6 |
7 |
8 |
5 |
6 |
7 |
8 |
|
|
0 |
1 |
2 |
1 |
0 |
5 |
0 |
1 |
2 |
3 |
|
|
2 |
3 |
4 |
3 |
3 |
7 |
4 |
3 |
4 |
5 |
9. Приводится статистический ряд случайной величины Х, имеющей нормальное распределение. Требуется:
1) найти точечные оценки параметров А и σ нормального распределения;
2) интервал ![]() , содержащий все наблюдаемые значения
, содержащий все наблюдаемые значения ![]() , разделить на 5 равных частей и построить гистограмму относительных частот. В качестве
, разделить на 5 равных частей и построить гистограмму относительных частот. В качестве ![]() и
и ![]() выбрать такие целые числа, чтобы интервал
выбрать такие целые числа, чтобы интервал ![]() имел наименьшую длину;
имел наименьшую длину;
3) записать функцию плотности распределения ![]() и построить её на одном чертеже с гистограммой.
и построить её на одном чертеже с гистограммой.
Все вычисления и построения в данной задаче допускается делать с использованием приложения MS Excel.
Результаты необходимо округлить до 0,001.
|
9.1. |
ХI |
3,1 |
3,7 |
4,3 |
4,9 |
5,5 |
6,1 |
6,7 |
7,3 |
7,9 |
8,5 |
|
Ni |
3 |
12 |
17 |
22 |
24 |
26 |
23 |
19 |
12 |
2 | |
|
9.2. |
ХI |
2,2 |
2,6 |
3,0 |
3,4 |
3,8 |
4,2 |
4,6 |
5,0 |
5,4 |
5,8 |
|
Ni |
4 |
8 |
10 |
13 |
16 |
14 |
11 |
10 |
9 |
5 | |
|
9.3. |
ХI |
2,9 |
3,7 |
4,5 |
5,3 |
6,1 |
6,9 |
7,7 |
8,5 |
9,3 |
10,1 |
|
Ni |
12 |
24 |
30 |
39 |
48 |
42 |
33 |
30 |
27 |
15 | |
|
9.4. |
ХI |
-1,6 |
-1,1 |
-0,6 |
-0,1 |
0,4 |
0,9 |
1,4 |
1,9 |
2,4 |
2,9 |
|
Ni |
5 |
14 |
19 |
24 |
26 |
28 |
25 |
21 |
14 |
4 | |
|
9.5. |
ХI |
-1,9 |
-1,3 |
-0,7 |
-0,1 |
0,5 |
1,1 |
1,7 |
2,3 |
2,9 |
3,5 |
|
Ni |
8 |
16 |
20 |
26 |
32 |
28 |
22 |
20 |
18 |
10 |
|
9.6. |
ХI |
3,4 |
4,2 |
5,0 |
5,8 |
6,6 |
7,4 |
8,2 |
9,0 |
9,8 |
10,6 |
|
Ni |
12 |
24 |
30 |
39 |
48 |
42 |
33 |
30 |
27 |
15 | |
|
9.7. |
ХI |
2,1 |
2,3 |
2,5 |
2,7 |
2,9 |
3,1 |
3,3 |
3,5 |
3,7 |
3,9 |
|
Ni |
8 |
16 |
20 |
26 |
32 |
28 |
22 |
20 |
18 |
10 | |
|
9.8. |
ХI |
5,1 |
5,7 |
6,3 |
6,9 |
7,5 |
8,1 |
8,7 |
9,3 |
9,9 |
10,5 |
|
Ni |
3 |
12 |
17 |
22 |
24 |
26 |
23 |
19 |
12 |
2 | |
|
9.9. |
ХI |
3,3 |
3,7 |
4,1 |
4,5 |
4,9 |
5,3 |
5,7 |
6,1 |
6,5 |
6,9 |
|
Ni |
4 |
8 |
10 |
13 |
16 |
14 |
11 |
10 |
9 |
5 | |
|
9.10. |
ХI |
0,4 |
0,9 |
1,4 |
1,9 |
2,4 |
2,9 |
3,4 |
3,9 |
4,4 |
4,9 |
|
Ni |
5 |
14 |
19 |
24 |
26 |
28 |
25 |
21 |
14 |
4 | |
|
9.11. |
ХI |
2,6 |
3,2 |
3,8 |
4,4 |
5,0 |
5,6 |
6,2 |
6,8 |
7,4 |
8,0 |
|
Ni |
3 |
12 |
17 |
22 |
24 |
26 |
23 |
19 |
12 |
2 | |
|
9.12. |
ХI |
0,2 |
0,6 |
1,0 |
1,4 |
1,8 |
2,2 |
2,6 |
3,0 |
3,4 |
3,8 |
|
Ni |
4 |
8 |
10 |
13 |
16 |
14 |
11 |
10 |
9 |
5 | |
|
9.13. |
ХI |
0,9 |
1,7 |
2,5 |
3,3 |
4,1 |
4,9 |
5,7 |
6,5 |
7,3 |
8,1 |
|
Ni |
12 |
24 |
30 |
39 |
48 |
42 |
33 |
30 |
27 |
15 | |
|
9.14. |
ХI |
2,4 |
2,9 |
3,4 |
3,9 |
4,4 |
4,9 |
5,4 |
5,9 |
6,4 |
6,9 |
|
Ni |
5 |
14 |
19 |
24 |
26 |
28 |
25 |
21 |
14 |
4 | |
|
9.15. |
ХI |
-3,9 |
-3,3 |
-2,7 |
-2,1 |
-1,5 |
-0,9 |
-0,3 |
0,3 |
0,9 |
1,5 |
|
Ni |
8 |
16 |
20 |
26 |
32 |
28 |
22 |
20 |
18 |
10 | |
|
9.16. |
ХI |
3,9 |
4,7 |
5,5 |
6,3 |
7,1 |
7,9 |
8,7 |
9,5 |
10,3 |
11,1 |
|
Ni |
12 |
24 |
30 |
39 |
48 |
42 |
33 |
30 |
27 |
15 | |
|
9.17. |
ХI |
5,1 |
5,3 |
5,5 |
5,7 |
5,9 |
6,1 |
6,3 |
6,5 |
6,7 |
6,9 |
|
Ni |
8 |
16 |
20 |
26 |
32 |
28 |
22 |
20 |
18 |
10 | |
|
9.18. |
ХI |
1,5 |
2,1 |
2,7 |
3,3 |
3,9 |
4,5 |
5,1 |
5,7 |
6,3 |
6,9 |
|
Ni |
3 |
12 |
17 |
22 |
24 |
26 |
23 |
19 |
12 |
2 | |
|
9.19. |
ХI |
4,4 |
4,8 |
5,2 |
5,6 |
6,0 |
6,4 |
6,8 |
7,2 |
7,6 |
8,0 |
|
Ni |
4 |
8 |
10 |
13 |
16 |
14 |
11 |
10 |
9 |
5 | |
|
9.20. |
ХI |
6,4 |
6,9 |
7,4 |
7,9 |
8,4 |
8,9 |
9,4 |
9,9 |
10,4 |
10,9 |
|
Ni |
5 |
14 |
19 |
24 |
26 |
28 |
25 |
21 |
14 |
4 |
| < Предыдущая | Следующая > |
|---|