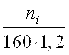13. Решение типовых задач (вариант контрольной)
Вариант № 0
0.1. Найти частные производные ![]() функции
функции
![]()
![]()
![]()
![]()
![]()
![]()
Ответ:
![]()
![]()
![]()
![]()
![]()
0.2. Найти экстремумы функции ![]()
1) Определяем критические точки. Для этого находим частные производные ![]() и решаем систему
и решаем систему 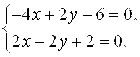
Решение этой системы: ![]() , значит
, значит ![]() – критическая (стационарная) точка.
– критическая (стационарная) точка.
2) Проверим выполнение достаточных условий экстремума. Находим частные производные 2-го порядка: ![]()
Вычисляем ![]()
Так как ![]() и
и ![]() то
то ![]() – точка максимума.
– точка максимума.
3) Экстремум функции – это значение функции в точке экстремума ![]() . Вычисляем это значение:
. Вычисляем это значение: ![]()
Ответ: ![]()
0.3. Вычислить двойной интеграл по области D, ограниченной указанными линиями. Сделать чертеж области.
![]()
Решение. Линия Y = – X2 – это парабола, а Y = – 5 – горизонтальная прямая. Найдем точки их пересечения. Для этого решим систему уравнений: 

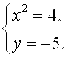

Изобразим область D В координатной плоскости.
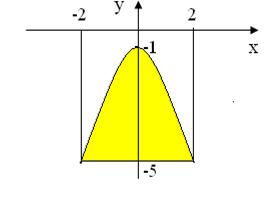
Расставим пределы интегрирования 
Вычислим двукратный интеграл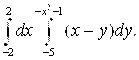
Интеграл 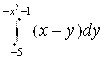 вычисляется в предположении, что X – Константа.
вычисляется в предположении, что X – Константа.


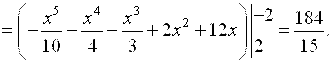
Ответ: 
0.4. Вычислить 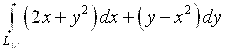 ,
,
Где ![]() – дуга параболы
– дуга параболы ![]() от точки A(0;0) до точки B(1;1).
от точки A(0;0) до точки B(1;1).
Решение. В данном случае АВ задана в виде: ![]() , где
, где ![]() , тогда
, тогда ![]() . Получим
. Получим

 .
.
Ответ: 
0.5. Найти интервал и область сходимости степенного ряда:  .
.
Решение. Фиксируем X и составляем ряд из модулей.  .
.
Применяем признак Даламбера для этого ряда:
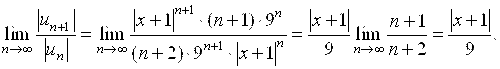
 при
при  ; |x + 1| < 9: –9 < x + 1 < 9; –10 < x < 8.
; |x + 1| < 9: –9 < x + 1 < 9; –10 < x < 8.
Значит, (–10, 8) – интервал абсолютной сходимости исходного ряда.
Исследуем поведение данного ряда на концах интервала сходимости.
При Х = –10: 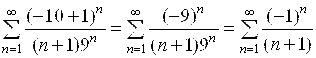 – этот ряд знакочередующийся. Применяем признак Лейбница:
– этот ряд знакочередующийся. Применяем признак Лейбница:
1) ![]() так как
так как ![]() ;
;
2) ![]() .
.
Следовательно, ряд 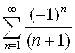 сходится по признаку Лейбница. Точка х = –10 входит в область сходимости степенного ряда
сходится по признаку Лейбница. Точка х = –10 входит в область сходимости степенного ряда 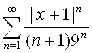 , в этой точке ряд сходится условно.
, в этой точке ряд сходится условно.
При Х = 8: 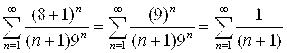 – этот ряд ведет себя так же, как гармонический ряд
– этот ряд ведет себя так же, как гармонический ряд ![]() , который расходится. Действительно, по предельному признаку
, который расходится. Действительно, по предельному признаку  . Значит, ряд
. Значит, ряд  расходится. Точка х = 8 не входит в область сходимости степенного ряда
расходится. Точка х = 8 не входит в область сходимости степенного ряда 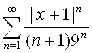 .
.
Областью сходимости ряда 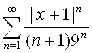 является интервал [–10, 8).
является интервал [–10, 8).
Ответ: интервал сходимости ряда (–10, 8),
Область сходимости ряда [–10, 8).
0.6. Используя разложение подынтегральной функции в степенной ряд, вычислить указанный определенный интеграл с точностью до 0,01:
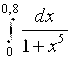 .
.
Решение. Разложим подынтегральную функцию в ряд Маклорена. При решении используем разложение:
 ,
,
В котором вместо X возьмем X5. Тогда
 .
.
Интеграл примет вид:


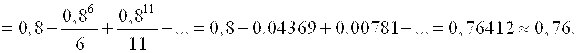
Для достижения указанной точности обычно оставляют первые несколько слагаемых ряда так, чтобы последнее из них было меньше этой точности. При вычислении оставляют на несколько знаков после запятой больше, чем требуется. В окончательном ответе округляют до указанной точности.
Ответ: 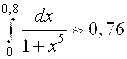 .
.
0.7. Разложить в ряд Фурье функцию ![]() , заданную на отрезке
, заданную на отрезке ![]()
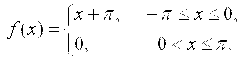 .
.
Решение. Здесь ![]() .
.
Вычислим коэффициенты Фурье:




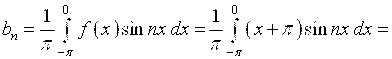
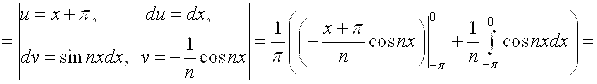

Ряд Фурье для данной функции запишется в виде
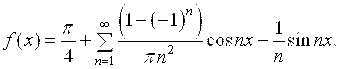
Ответ: 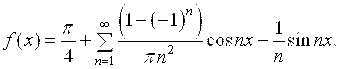
0.8. Вероятность изготовления детали высшего качества равна 0,8. Найти вероятность того, что среди 9 наудачу взятых деталей будет от 5 до 7 деталей высшего качества. Вычисления производить с точностью до 0,001.
Решение.
Эта задача подчиняется схеме повторений испытаний, в которой событие А состоит в выборе детали высшего качества. Здесь N=9; P=0,8; K1=5; K2=7. Требуется найти вероятность того, что событие А произойдет от K1 до K2 раз в этих N испытаниях – ![]() . Так как N < 30, то применим формулу Бернулли:
. Так как N < 30, то применим формулу Бернулли:

Ответ: вероятность равна 0,544.
0.9. Приводится статистический ряд случайной величины Х, имеющей нормальное распределение. Требуется:
1) найти точечные оценки параметров А и σ нормального распределения;
2) интервал ![]() , содержащий все наблюдаемые значения
, содержащий все наблюдаемые значения ![]() , разделить на 5 равных частей и построить гистограмму относительных частот. В качестве
, разделить на 5 равных частей и построить гистограмму относительных частот. В качестве ![]() и
и ![]() выбрать такие целые числа, чтобы интервал
выбрать такие целые числа, чтобы интервал ![]() имел наименьшую длину;
имел наименьшую длину;
3) записать функцию плотности распределения ![]() и построить её на одном чертеже с гистограммой.
и построить её на одном чертеже с гистограммой.
Все вычисления и построения в данной задаче допускается делать с использованием приложения MS Excel.
Результаты необходимо округлить до 0,001.
|
ХI |
1,3 |
1,9 |
2,5 |
3,1 |
3,7 |
4,3 |
4,9 |
5,5 |
6,1 |
6,7 | |
|
Ni |
2 |
10 |
17 |
21 |
26 |
25 |
24 |
18 |
14 |
3 |
Решение. 1) Объём выборки ![]() .
.
Параметры нормального распределения А и ![]() равны математическому ожиданию и среднему квадратическому отклонению соответственно:
равны математическому ожиданию и среднему квадратическому отклонению соответственно:
![]()
Оценками для них являются выборочное среднее и выборочное среднее квадратическое отклонение. Найдем их:
![]() ,
,
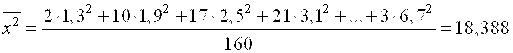 ,
,
![]() ,
, ![]() .
.
2) Выберем ![]() =1,
=1, ![]() =7. тогда
=7. тогда ![]() . Составим Группированный статистический ряд:
. Составим Группированный статистический ряд:
|
Интервалы |
|
|
|
|
|
|
Ni |
12 |
38 |
51 |
42 |
17 |
Для построения гистограммы составим вспомогательную таблицу
|
Интервалы |
|
|
|
|
|
|
|
0,062 |
0.198 |
0.266 |
0.219 |
0.088 |
Строим гистограмму:

3) Запишем функцию плотности распределения
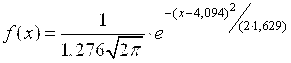 .
.
Построим её на одном чертеже с гистограммой. Для этого вычислим значения функции в серединах интервалов, отметим эти точки на графике и соединим их плавной линией.
Ответ: 1) ![]() ,
, ![]() 3)
3) 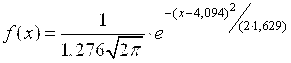 .
.
| < Предыдущая |
|---|