11. Математическая статистика

Выборочной совокупностью (или просто выборкой) называют совокупность из случайно отобранных объектов. Генеральной совокупностью называют совокупность объектов, из которых производится выборка.

Объём генеральной совокупности N и объем выборки N – число объектов в рассматриваемой совокупности.

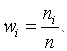Пусть интересующая нас случайная величина Х принимает значение Х1 в выборке П1 раз, Х2 – П2 раз, …, Хк – пк раз, причем где П – объем выборки. Тогда наблюдаемые значения случайной величины Х1, Х2,…, Хк называют вариантами, а П1, П2,…, Пк – частотами. Если разделить каждую частоту на объем выборки, то получим относительные частоты Перечень вариант и соответствующих им частот или относительных частот называют статистическим рядом:

Xi	X1	X2	…	Xk
Ni	N1	N2	…	Nk

Xi	X1	X2	…	Xk
Wi	W1	W2	…	Wk

Или

Если исследуется некоторый непрерывный признак, то статистический вариационный ряд может состоять из очень большого количества чисел. В этом случае удобнее использовать группированную выборку. Для ее получения интервал , в котором заключены все наблюдаемые значения признака, разбивают на K равных частичных интервалов длиной , а затем для каждого частичного интервала I Находят Ni – сумму частот вариант, попавших в этот интервал. Составленная по этим результатам таблица называется Группированным статистическим рядом:

Интервалы			…
Ni	N1	N2	…	Nk

Гистограмма.

Для наглядного представления о поведении исследуемой случайной величины в выборке служит гистограмма, то есть ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиной H, а высотами – отрезки длиной (гистограмма частот) или (гистограмма относительных частот). В первом случае площадь гистограммы равна объему выборки, во втором – единице.

Числовые характеристики статистического распределения.

1. Выборочным средним называется среднее арифметическое значений случайной величины, принимаемых в выборке:

,

Где Xi – варианты, Ni – частоты.

Выборочное среднее служит для оценки математического ожидания исследуемой случайной величины.

2. Выборочной дисперсией называется

,

Где

Выборочная дисперсия служит для оценки дисперсии исследуемой случайной величины.

3. Выборочным средним квадратическим отклонением называется

.

< Предыдущая		Следующая >