10. Случайные величины

Случайной величиной (СВ) называют величину, которая в результате испытания (опыта, наблюдения, измерения) примет одно из своих возможных значений.

Случайные величины обозначают , , , ,…

СВ бывают дискретными или непрерывными. Дискретная СВ принимает отдельные, изолированные значения. Непрерывная СВ может принимать любое значение из конечного или бесконечного интервала. Существуют смешанные СВ.

Функция распределения СВ F(X) есть вероятность того, что случайная величина в результате опыта приняла значение меньшее числа Х:

.

Свойства:

1. ;

2. , при ( – неубывающая функция);

3. , ;

4. .

Законом распределения СВ называют правило, позволяющее находить вероятности отдельных значений случайной величины или множества этих значений.

Закон распределения дискретной СВ можно задать таблицей распределения:

Х			…
Р			…

Где – возможные значения Х, а – вероятности событий .

Свойства:

1. 2. .

Закон распределения непрерывной СВ можно задать функцией плотности распределения .

Свойства:

1. ; 2. ;

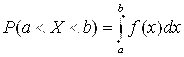3. ; 4.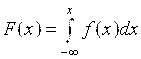

Числовые характеристики случайных величин

1. Математическое ожидание случайной величины Х.

Для дискретной СВ: .

Для непрерывной СВ: .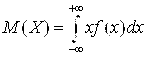

2. Дисперсия случайной величины Х:

.

Для дискретной СВ: .

Для непрерывной СВ: .

Свойства дисперсии:

1) Дисперсия постоянной величины равна нулю, т. е. .

2) Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат, т. е.

3) Дисперсия суммы (разности) двух независимых величин равна сумме дисперсий этих величин, т. е.

3. Среднее квадратическое отклонение СВ:

Некоторые часто встречающиеся непрерывные случайные величины.

1) Равномерное распределение.

Случайная величина имеет равномерное распределение на интервале , если плотность распределения задается формулой

Функция распределения вероятностей имеет вид:

.

Числовые характеристики: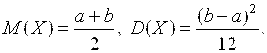

2) Показательное распределение.

Случайная величина Х имеет показательное распределение, если плотность распределения задается формулой

Где – константа (параметр распределения).

Функция распределения имеет вид

Числовые характеристики:

3) Нормальное распределение.

Случайная величина Х имеет нормальное распределение, если плотность распределения задается формулой

Где А и – параметры распределения (константы).

Функция распределения имеет вид

.

Числовые характеристики:

Вероятность того, что Х примет значение из интервала вычисляется по формуле

,

Где – функция Лапласа.

< Предыдущая		Следующая >