09. События, вероятность событий
События подразделяются на случайные (обозначаются A, B, A1, A2, …), достоверные (обозначаются ![]() ), невозможные (обозначаются Æ).
), невозможные (обозначаются Æ).![]()
Событие, состоящее в том, что событие А не наступило, называют Противоположным ![]() и обозначают
и обозначают ![]()
Событие, состоящее в наступлении А или B, называют Суммой событий и обозначают ![]() .
.
Событие, состоящее в наступлении А и B, называют Произведением событий и обозначают ![]() .
.
Если ![]() , то события А и
, то события А и ![]() – Несовместные, если
– Несовместные, если ![]() , то события
, то события ![]() и
и ![]() – Совместные.
– Совместные.
Вероятность события A обозначается ![]() и является численным выражением возможности наступления A.
и является численным выражением возможности наступления A.
Свойства вероятности:
![]() ,
, ![]()
![]()
![]()
Классическое определение вероятности события:
![]() ,
,
Где N – общее число всех элементарных равновозможных исходов испытания, образующих полную группу попарно несовместных событий, а M – число исходов, благоприятствующих появлению события ![]()
Вероятность произведения событий.
Вероятность события В при условии, что произошло событие А называют условной вероятностью и обозначают ![]() или
или ![]()
Вероятность произведения событий A и B Вычисляется по формуле:
![]() .
.
Событие B Называется Независимым От события A, Если его условная вероятность равна безусловной, т. е. ![]() . Если событие B не зависит от события A, То и событие A Не зависит от события B.
. Если событие B не зависит от события A, То и событие A Не зависит от события B.
Если ![]() и
и ![]() – независимые события, то
– независимые события, то
![]() .
.
Вероятность суммы событий:
Если ![]() и
и ![]() – несовместные, то
– несовместные, то ![]() ,
,
Если ![]() и
и ![]() – совместные, то
– совместные, то ![]()
Формула полной вероятности. Формула Байеса.
Если событие А может произойти только вместе с одним из попарно несовместных событий ![]() образующих полную группу событий, то вероятность события А вычисляется по формуле, называемой Формулой полной вероятности:
образующих полную группу событий, то вероятность события А вычисляется по формуле, называемой Формулой полной вероятности:
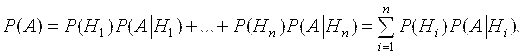
События ![]() называют гипотезами.
называют гипотезами.
Для нахождения условных вероятностей гипотез пользуются Формулой Байеса:
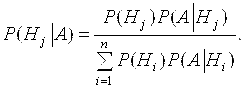
Схема повторений испытаний.
Пусть производится N независимых испытаний, в каждом из которых событие А может произойти с одной и той же вероятностью Р. Требуется найти:
• вероятность того, что событие А произойдет ровно K раз в этих N испытаниях – ![]() ;
;
• вероятность того, что событие А произойдет от K1 До K2 раз в этих N испытаниях – ![]()
При различных P и N используются разные формулы.
Формула Бернулли (используется при N<30; для больших значений N процесс вычислений затруднен из-за громоздкости, а часто просто практически невозможен):
![]()
 ,
,
Где ![]() – число сочетаний.
– число сочетаний.
Формулы Муавра-Лапласа (при больших N и 0,1<P<0,9):
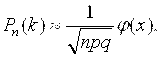
![]() ,
,
Где 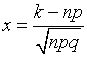 ,
, 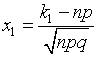 ,
, 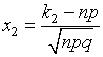 ,
,  ,
, 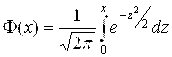 – функция Лапласа (значения функций
– функция Лапласа (значения функций ![]() и
и ![]() можно найти по таблице из [4], [6]).
можно найти по таблице из [4], [6]).
Формула Пуассона (при больших N и P<0,1):
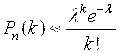 ,
,
 , где
, где ![]() .
.
| < Предыдущая | Следующая > |
|---|