06. Функциональные ряды
Ряд  , членами которого являются функции
, членами которого являются функции ![]() , называется Функциональным.
, называется Функциональным.
Область сходимости функционального ряда
Множество значений X, при которых функциональный ряд  сходится, называется областью сходимости этого ряда.
сходится, называется областью сходимости этого ряда.
Степенные ряды
Функциональный ряд вида
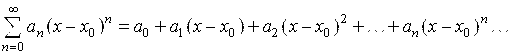 ,
,
Где A0, A1, A2, …, An , … , Х0 – числа, называется Степенным рядом. Числа A0, A1, A2, …, An , … называются коэффициентами этого ряда.
Теорема Абеля. Пусть степенной ряд 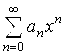 сходится при X1 ≠ 0 и расходится при X2. Тогда он сходится при всех X удовлетворяющих условию:
сходится при X1 ≠ 0 и расходится при X2. Тогда он сходится при всех X удовлетворяющих условию: ![]() И расходится при всех X, удовлетворяющих условию:
И расходится при всех X, удовлетворяющих условию: ![]() .
.
Радиус, интервал и область сходимости степенного ряда
Число R Называется радиусом сходимости степенного ряда , если ряд сходится для всех X, удовлетворяющих условию
, если ряд сходится для всех X, удовлетворяющих условию ![]() и расходится для всех X, удовлетворяющих условию
и расходится для всех X, удовлетворяющих условию ![]() . Интервал (X0 – R, X0 + R), где R – радиус сходимости ряда
. Интервал (X0 – R, X0 + R), где R – радиус сходимости ряда  называется интервалом сходимости данного степенного ряда. Внутри интервала сходимости степенной ряд сходится, а вне него расходится. На концах интервала сходимости ряд может сходиться, а может и расходиться. Концы интервала сходимости ряда исследуются особо. Областью сходимости степенного ряда является интервал сходимости данного ряда вместе с концами этого интервала, в которых данный ряд сходится.
называется интервалом сходимости данного степенного ряда. Внутри интервала сходимости степенной ряд сходится, а вне него расходится. На концах интервала сходимости ряд может сходиться, а может и расходиться. Концы интервала сходимости ряда исследуются особо. Областью сходимости степенного ряда является интервал сходимости данного ряда вместе с концами этого интервала, в которых данный ряд сходится.
Ряд Тейлора. Ряд
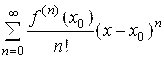
Называется рядом Тейлора функции F.
Ряд Тейлора функции F , когда X0 = 0, называется рядом Маклорена этой функции.
Ниже приведены ряды Маклорена для некоторых функций с областями их сходимости:
1) 
2) 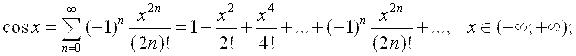
3) 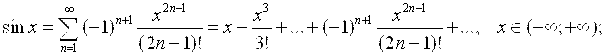
4) 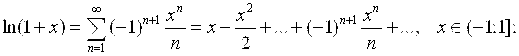

При ![]() получаем
получаем
 ,
,
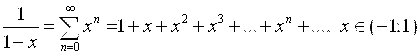 .
.
6)  .
.
| < Предыдущая | Следующая > |
|---|