05. Числовые ряды
Числовым рядом называется выражение вида 
, где U1, U2, …, Un, … – числа.
называется N– ой Частичной суммой ряда.
Если существует конечный предел 
, то ряд 
Называется Сходящимся, а S – его суммой. В противном случае ряд Называется Расходящимся.
Необходимое условие сходимости ряда. Если ряд Сходится, то 
. Необходимое условие не является достаточным!
Достаточное условие расходимости ряда. Если 
, то ряд Расходится.
Геометрическая прогрессия – это ряд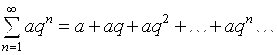 
Он сходится при 
(его сумма равна в этом случае 
) и расходится при 
.
Ряд 
называется Рядом Дирихле. Он сходится при P >1 и расходится при P ≤ 1.
Ряд называется Знакоположительным, если Un > 0 для всех NÎN.
Признак сравнения знакоположительных рядов. Пусть и 
– два знакоположительных ряда и 
для всех NÎN. Тогда
1) если ряд Сходится, то ряд Сходится;
2) если ряд Расходится, то ряд расходится.
Предельный признак сравнения знакоположительных рядов.
Пусть и 
– знакоположительные ряды и существует конечный предел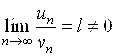 
. Тогда ряды , сходятся или расходятся одновременно.
Признак Даламбера. Пусть– знакоположительный ряд и существует конечный предел 
. Тогда
1) если L < 1, то ряд сходится;
2) если L >1. то ряд расходится.
Признак Коши. Пусть– знакоположительный ряд и существует конечный предел 
. Тогда
1) если L < 1, то ряд сходится:
2) если L >1. то ряд расходится.
Интегральный признак сравнения знакоположительных рядов. Пусть функция F – непрерывна, положительна и убывает на интервале (1, ∞) и 
. Тогда
1) если интеграл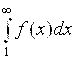 
сходится, то ряд Тоже сходится;
2) если интеграл 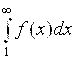расходится, то ряд Тоже расходится.
Знакопеременные ряды
Ряд называется знакопеременным, если среди его членов есть как положительные, так и отрицательные.
Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд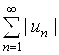 
, составленный из абсолютных величин этого ряда. Если ряд сходится, а ряд 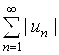, составленный из абсолютных величин этого ряда, расходится, то ряд Называется условно сходящимся. Если ряд сходится абсолютно, то он сходится.
Знакочередующиеся ряды
Ряд называется знакочередующимся, если он имеет вид:
.
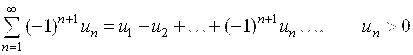Признак сходимости Лейбница.
Если в знакочередующемся ряде 
и 
, то ряд сходится, причем его сумма S удовлетворяет условию |S| ≤ |U1|.
| < Предыдущая | Следующая > |
|---|
