04. Кратные и криволинейные интегралы

Двойной интеграл в декартовых координатах

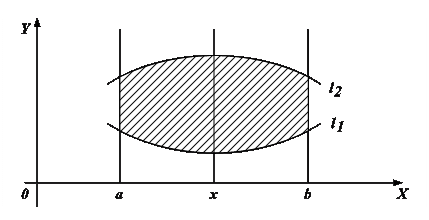
Пусть область D ограничена линиями:

;

, (),

При этом прямые пересекают границы области D не более, чем в двух точках. Тогда

Площадь плоской области D находится по формуле

Двойной интеграл в полярных координатах

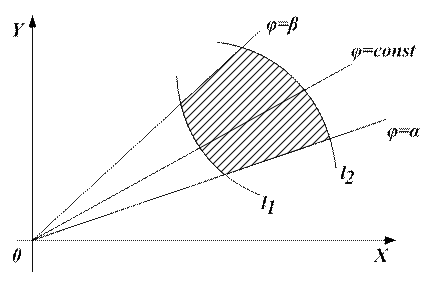
Пусть область D ограничена линиями:

Тогда

Вычисление объема тела

Если тело ограничено снизу графиком функции Z=F1(X, Y), сверху графиком функции Z=F2(X, Y), с боков цилиндрической поверхностью с образующими параллельными оси OZ и направляющей, которая является границей области D Из плоскости ОХу, то объем этого тела вычисляется по формуле:

Криволинейный интеграл второго рода (по координатам)

Где AB – плоская кривая, соединяющая точки и .

Если AB задана как функция Y От переменной X:

то

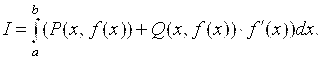
Если AB задана как функция X От переменной Y:

то .

Если AB задана параметрически: , то

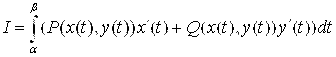
Если 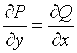, то интеграл не зависит от вида кривой и вычисляется по формуле:

.

Для восстановления используются формулы:

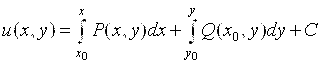
Или

,

Где – точка непрерывности функций и их частных производных.

< Предыдущая		Следующая >