03. Функции нескольких переменных

Выражение – Функция двух независимых переменных X И Y. Область определения функции – это множество точек (X,Y) плоскости XOY, в которых функция определена.

Частная производная функции Z По переменной X:

;

Частная производная функции Z По переменной Y:

.

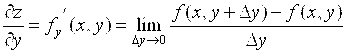Все правила дифференцирования функций остаются справедливыми и при нахождении частных производных, только надо помнить, что при отыскании переменная Y Считается постоянной, а при отыскании переменная X Считается постоянной.

Частные производные второго порядка – это производные от первых производных: .

Экстремумы функции двух переменных

Функция имеет Максимум в точке если для любой точки из окрестности точки , и имеет Минимум в точке если для любой точки из окрестности точки .

Значения функции в точках максимума и минимума называют Экстремумами функции.

Схема определения экстремума:

1. Найти стационарные (критические) точки. Это точки, в которых частные производные и Равны нулю или не существуют (это необходимые условия экстремума).

2. Для каждой стационарной точки проверить выполнение достаточных условий экстремума. Для этого найти частные производные второго порядка и вычислить их значения в стационарной точке :

Если то – точка максимума функции при , или точка минимума функции при

Если то экстремума нет.

< Предыдущая		Следующая >