07. Ряды Фурье

Пусть функция F(X) удовлетворяет следующим условиям:

• она непрерывна на интервале , за исключением может быть конечного числа точек разрыва первого рода,

• она имеет на интервале лишь конечное число экстремумов.

Тогда F(X) может быть представлена в виде ряда Фурье, который сходится к ней в точках ее непрерывности и сходится к среднему арифметическому правого и левого пределов этой функции в точках разрывов функции. Ряд Фурье имеет вид:

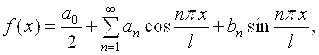
Где 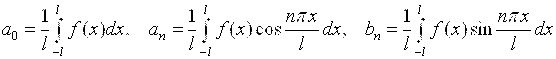– коэффициенты Фурье функции F(X).

Если функция F(X) – четная, то коэффициенты Фурье примут вид:

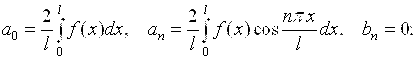
Получим 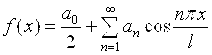– ряд Фурье по косинусам.

Если функция F(X) – нечетная, то коэффициенты Фурье примут вид:

Получим – ряд Фурье по синусам.

Если F(X) определена на интервале , то её можно доопределить на четным образом и разложить в ряд Фурье по косинусам, или нечетным образом и разложить в ряд Фурье по синусам.

При вычислении коэффициентов ряда полезно использовать формулы:

, , .

< Предыдущая		Следующая >