30. Системы дифференциальных уравнений. Общие определения. Нормальные системы уравнений
ОпреДеление. Системой дифференциальных уравнений называется совокупность уравнений, в каждое из которых входят независимая переменная, искомые функции и их производНЫе.
Всегда предполагается, что число уравнений равно числу неизвестных функций.
Например, система двух дифференциальных уравнений первого порядка имеет вид
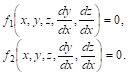
Наша задача состоит в том, чтобы найти функции ![]() и
и ![]() , удовлетворяющие обоим уравнениям. С системами дифференциальных уравнений мы сталкиваемся при изучении процессов, для описания которых одной функции недостаточно. Мы видели, что отыскание векторных линий поля приводит нас к системе дифференциальных уравнений. Ранее было отмечено, что изучение динамики криволинейного движения требует решения системы трех дифференциальных уравнений, в которых неизвестными функциями являются проекции движущейся точки на оси координат, а независимой переменной—время.
, удовлетворяющие обоим уравнениям. С системами дифференциальных уравнений мы сталкиваемся при изучении процессов, для описания которых одной функции недостаточно. Мы видели, что отыскание векторных линий поля приводит нас к системе дифференциальных уравнений. Ранее было отмечено, что изучение динамики криволинейного движения требует решения системы трех дифференциальных уравнений, в которых неизвестными функциями являются проекции движущейся точки на оси координат, а независимой переменной—время.
В настоящем параграфе будут рассмотрены некоторые простейшие системы дифференциальных уравнений.
Определение. Нормальной системой дифференциальных уравнений называется система уравнений вида
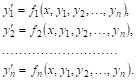 (*)
(*)
Решением такой системы называется совокупность П функций ![]() удовлетворяющих всем уравнениям системы.
удовлетворяющих всем уравнениям системы.
Частным решением системы (*) называется решение, удовлетворяющее заданным начальным условиям
![]()
Где ![]() — Заданные постоянные величины.
— Заданные постоянные величины.
Покажем, не приводя доказательства, что, как правило, данную систему дифференциальных уравнений можно привести к нормальной, ей эквивалентной.
1. Приведем к нормальной систему линейных уравнений
![]()
Разрешив данные уравнения относительно производных ![]() и
и ![]() :
:
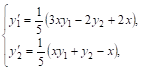
Мы и получаем нормальную систему.
2. Систему уравнений
![]()
Нельзя разрешить относительно ![]() и
и ![]() . Следовательно, эту систему нельзя привести к нормальной. Подобные системы мы Рассматривать не будем.
. Следовательно, эту систему нельзя привести к нормальной. Подобные системы мы Рассматривать не будем.
3. Приведем к нормальной систему уравнений
![]()
Здесь для приведения системы к нормальной мы введем вспомогательные функции ![]() и
и ![]() . Тогда
. Тогда ![]() ,
, ![]() И заданная система заменится следующей:
И заданная система заменится следующей:
![]()
Полученная система уже является нормальной.
Покажем теперь, что одно дифференциальное уравнение N-го порядка, разрешенное относительно старшей производной, с помощью введения новых вспомогательных функций всегда можно свести к нормальной системе дифференциальных уравнений.
Возьмем, например, уравнение третьего порядка
![]()
И введем две новые вспомогательные функции
![]()
Тогда заданное уравнение заменится системой трех уравнений
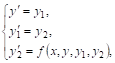
Которая является частным случаем нормальной системы (*). Ясно, что так можно поступать в случае уравнения любого порядка П; При этом число вспомогательных функций будет равно N-1.
В обычно встречающихся случаях верно и обратное утверждение:
Нормальная система уравнений может быть заменена однИМ дифференциальным уравнением, порядок которого равен числУ Уравнений системы.
Рассмотрим, например, систему уравнений
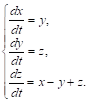
Продифференцируем первое уравнение по переменной T и ЗАменим производную ![]() ее выражением из второго уравнения:
ее выражением из второго уравнения:
![]()
Продифференцируем еще раз это уравнение и заменим производную ![]() ее выражением из третьего уравнения:
ее выражением из третьего уравнения:
Так как ![]() , А
, А ![]() , то окончательно получим:
, то окончательно получим:
![]()
Или
![]()
Т. Е. линейное дифференциальное уравнение третьего порядка с постоянными коэффициентами.
Обращаем внимание читателя, что в процессе исключения функций У и Z мы выражаем их через функцию Х и ее производные. Найдя общее решение полученного дифференциального уравнения высшего порядка, мы получим выражение для функции Х, зависящее от трех произвольных постоянных. Остальные неизвестные функции (У и Z) находятся уже не при помощи интегрирования, а из их выражений через найденную функцию. Таким образом, общее число произвольных постоянных не увеличится и будет равно порядку системы. Решим полученное уравнение третьего порядка
![]()
Характеристическое уравнение, ему соответствующее: ![]() , имеет корни
, имеет корни ![]() Следовательно,
Следовательно,
![]()
Поскольку при исключении У и Z мы получали ![]() и
и ![]() , то
, то
![]()
На основании рассмотренного примера МЫ сделаем следующий вывод (доказательство его мы опускаем):
Общее решение нормальной системы
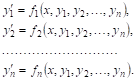 (*)
(*)
Имеет вид
![]()
Где ![]() - произвольные постоянные.
- произвольные постоянные.
Задаваясь начальными условиями, мы получаем П уравнений для определения этих произвольных постоянных:
 (**)
(**)
Для нормальных систем уравнений также имеет место теорема, гарантирующая существование и единственность частного решения.
Теорема. Если правые части нормальной системы непрерывны вместе со своими частными производными при значениях ![]() , то существует единственная система функций
, то существует единственная система функций ![]() , являющаяся решением системы и удовлетворяющая заданным начальным условиям.
, являющаяся решением системы и удовлетворяющая заданным начальным условиям.
| < Предыдущая | Следующая > |
|---|