31. Системы линейных дифференциальных уравнений с постоянными коэффициентами

В приложениях особенно часто встречаются системы линейных уравнений с постоянными коэффициентами. Для большей краткости изложения ограничимся рассмотрением нормальной системы трех однородных уравнений с тремя неизвестными функциями и . Запишем эту систему в виде

(*)

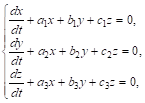Где — Постоянные величины.

Предлагаем читателю самостоятельно доказать следующие простые свойства этой системы:

1) Если известна частная система решений Системы УРавнениИ (*), то функции где С — произвольная постоянная, также образуют систему решений.

2) Если известны две системы решений и , То и функции

Также являются решениями.

Отсюда следует, что если известны три системы частных решеНИй , и , то функции

(**)

Представляют систему решений при любых постоянных и . Выясним, в каком случае из нее можно получить частное решение, удовлетворяющее любым заданным начальным условиям. Если эти условия таковы:

То система уравнений для определения постоянных примет вид

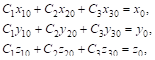
Где — Значения соответствующих функций при . Для того чтобы эта система имела единственное решение при любых начальных условиях, необходимо и достаточно, чтобы определитель

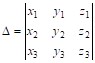
Ни при каком значении не обращался в нуль. Мы, как и раньше, будем говориТь, что совокупность трех систем частных решений, удовлетворяющих этому условию, образует Фундаментальную систему.

Чтобы свести систему (*) к одному уравнению третьего порядка, мы должны продифференцировать одно из этих уравнений, наПРимер первое. При этом все последовательные производные функции Х Будут линейно выражаться через функции Х, у и Z. Поэтому и, наоборот, функции У и Z линейно выразятся черЕЗ Х, и . Отсюда следует, что в результате мы получим линейное дифференЦиальное уравнение с постоянными коэффициентами. Так как струкТУру решений такого уравнения мы знаем, то практически целесообразно не сводить систему к одному уравнению, а прямо искать частные решения системы в виде

(***)

Где и R — неопределенные постоянные коэффициенты, которые следует определить.

Дифференцируя функции Х, у и Z и подставляя в систему (*), Получим:

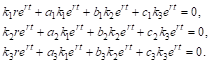
Сократив на , мы придем к системе линейных однородных уравнений относительно и :

(****)

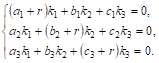Чтобы эта система однородных уравнений имела ненулевые решения (только такие нас и интересуют), необходимо и достаточно, чтобы ее определитель был равен нулю:

Раскрыв этот определитель, мы получим уравнение третьей степени относительно R. Это уравнение называется Характеристическим.

Итак, для того чтобы существовало решение вида (***), необходимо и достаточно, чтобы число R было корнем характеристического уравнения.

Мы в дальнейшем будем предполагать, что характеристическое уравнение имеет только простые корни. (Случай кратных корней более сложен, и мы его опускаем.)

Допустим, что один из действительных корней равен . Подставив это значение в систему уравнений (****), получим:

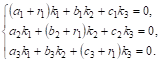
Определитель этой системы по условию равен нулю. Можно доказать, что если — простой корень характеристического уравнения (а только такие корни мы и условились рассматривать), то по крайней мере один из миноров второго порядка этого определителя не равен нулю. Тогда одно из уравнений является следствием двух остальных и система сводится к двум уравнениям с тремя неизвестными. Решение такой системы будет зависеть от одной произвольной постоянной. Если, например, система сводится к двум первым уравнениям, то одним из решений будут числа

Все остальные решения получаются умножением чисел и на одну и ту же произвольную постоянную. Поступая так со всеми корнями характеристического уравнения, мы найдем три системы функций, каждая из которых является решением системы (*).

Эти системы функЦИй таковы:

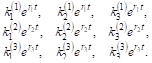
Доказательство того, что эти функции образуют фундаментальную систему, мы опускаем.

Тогда общее решенИЕ системы (*) запишется в виде

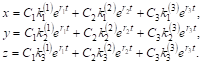
В случае комплексно сопряженных корней характеристического уравнения действительные решения, так же как и для случая оДНого дифференциального уравнения, имеют вид и . В этом случае уДОбнее сразу записать, что (т. Е. положить ), и находить функции , выражая их через функции Х1 и Х2 и их производные, как это было указано ранее. Легко заметить, что кажДАя из искомых функций будет линейной комбинацией Х1 и Х2.

Примеры. 1) Решим систему

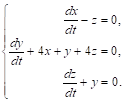
Система уравнений (****) имеет вид

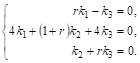
Составим характеристическое уравнение:

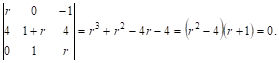
Его корни:

Здесь удобнее взять первое и третье уравнения системы относительно

Для

Одним из решений этой системы будут числа

Следовательно,

Для

Здесь можно положить

Тогда

Наконец, для

Выбирая

Получим:

Окончательно общее решение системы таково:

Предоставляем читателю проверить, что найденная система частных решений является фундаментальной.

2) Решим систему

Характеристическое уравнение системы имеет вид

Откуда

Следовательно, и . Из первого уравнения имеем:

Подставляя вместо Х найденное выражение, получим:

Легко проверить, что эти решения образуют фундаментальную систему и, следовательно, общим решением системы будет

Если дана система однородных линейных уравнений с постоянными коэффициентами, не приведенная к нормальной (система может быть любого порядка), то и к ней можно применить указанный метод. Ограничимся рассмотрением примера.

Пусть дана система уравнений второго порядка

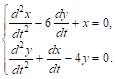
Полагая , придем к системе уравнений

Рассуждая так же, как и раньше, приходим к характеристическому уравнению

Его корни:

Можно прямо записать, что

Чтобы найти функцию У, выразим ее через Х. Дифференцируя ПерВое уравнение и подставляя значение во второе, получим:

Выполнив дифференцирование, найдем У:

Рассмотрим в заключение одну задачу из электротехники, которая приведет нас к системе линейных уравнений с постоянными коэффициентами.

Пусть даны две цепи; их сопротивление, самоиндукцию и емкость обозначим соответственно через для первой цепи и через — для второй. Предположим, далее, что цепи находятся в электромагнитной связи: каждая индуцирует электродвижущую силу другой. Если обозначить через М постоянный коэффициент взаимной индукции, то оказывается, что индУЦированное напряжение первой цепи будет равно , второй — , где обозначают силу тока соответственно в первой и во второй цепях.

Предположим, что в обеих цепях отсутствует вНЕшняя электродвижущая сила. При этом течение тока в цепяХ будет регулироваться следующими дифференциальными уравнениями:

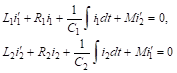
Или, после дифференцирования по T,

Мы получили систему двух дифференциальных уравнений второго порядка.

Составим ХАрактеристическое уравнение:

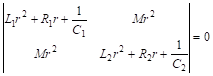
Или

На практике обычно оказывается, что это уравнение имеет две пары комплексно сопряженных корней, т. е. колебания тока в цепях будут складываться из двух гармонических колебаний (вообще говоря, затухающих). Подробный анализ всех встречающиХСя при этом случаев приводится в курсах электротехники. Отметим еще, что если не учитывать емкостей в цепях, то течение тока будет описываться системой уравнений первого порядка.

< Предыдущая