29. Колебания. Резонанс

I. Механические колебания. Задачи о колебаниях занимают значительное место в ряду важных задач современной техники и физики. В большом числе случаев явления колебаний описываются линейными дифференциальными уравнениями второго порядка (линейные колебания), которые в простейших условиях имеют постоянные коэффициенты. Рассмотрим сначала механические колебания.

Допустим, что на движущееся тело (массу для простоты будем считать равной единице) действует сила, стремящаяся вернуть тело в состояние равновесия, причем величина силы пропорциональна отклонению от положения равновесия. Если обозначить через S расстояние тела от положения равновесия, а через — коэффициент пропорциональности, то величина силы будет равна . Указанная сила называется восстанавливающей силой; W называется коэффициентом восстановления.

Далее, пусть движение происходит при наличии сопротивления среды. Силу, возникающую при этом, предположим пропорциональной скорости движения. Она направлена в сторону, обратную направлению движения, а ее величина равна , если через 2K обозначить коэффициент пропорциональности. Эта сила называется силой сопротивления, а K — коэффициентом сопротивления.

Наконец, допустим, что на систему действует посторонняя заданная сила , выраженная как функция времени T. Ее называют возмущающей силой (точнее, внешней возмущающей силой).

Составим Дифференциальное уравнение движения. Для получения равнодействующей всех сил нужно, очевидно, восстанавливающую силу и силу сопротивления взять со знаком минус, ибо первая направлена в сторону, противоположную направлению отсчета S, а вторая противоположна скорости. Таким образом, приходим к уравнению

Или

(*)

Итак, Указанные явления механических колебаний описываются линейными дифференциальными уравнениями второго порядка с постоянными коэффициентами.

Если внешняя возмущающая сила отсутствует , то колебание называется свободным или собственным; свободному КОлебанию отвечает однородное уравнение, соответствующее уравнению (*). При наличии возмущающей силы говорят, что КолеБание вынужденное; такое колебание описывается неоднородным уравнением (*), правая часть которого называется иногда возмущающим членом.

Восстанавливающей силой может быть сила упругости. Реально такой случай осуществляется, например, при следующих обстоятельствах. К вертикальной пружине подвешен груз, в точности уравновешивающийся силой упругости пружины. Если груз выводится вертикальной силой из состояния равновесия, то в дальнейшем он будет совершать колебания — свободные при отсутствии дополнительной силы, действующей на груз или на всю систему, вынужденные при наличии ее (например, когда сама точка привеса пружины по некоторому закону перемещается по вертикали). Сила противодействия пружины (восстанавливающая сила) будет действительно пропорциональна отклонениям (деформациям), как это следует из закона Гука. Коэффициент восстановления есть «жесткость» пружины.

II. Исследование свободных колебаний. Обратимся к применениям известных нам решений линейных уравнений с постоянными коэффициентами к исследованию колебаний. Начнем со свободных колебаний

Характеристическое уравнение имеет корни: . Возможны три случая.

1) Коэффициент сопротивления больше коэффициента восстановления: .

При этом решением будет

Где .

Мы видим, что никакого Колебания не происходит; с увеличением T отклонение S уменьшается, стремясь к нулю при и система монотонно стремится к равновесию (которое практически наступает в конечный момент времени). Мы имеем дело с НепериодичЕсКим и, как говорят, затухающими движениями. Наглядно этот случай можно объяснить тем, что влияние силы сопротивления (тормозящей движение) настолько превосходит влияние силы восстановления (вызывающей колебания), что движение затухает до того, как система перейдет положение равновесия.

2) Коэффициент сопротивления равен коэффициентУ восстановления: .

При этом решением будет

Этот случай не отличается от предыдущего в том смысле, что S является, начиная с некоторого T, убывающей функцией и при .

3) КоЭФфициент сопротИВления меньше коЭФфициента восстановления: .

При этом решением будет

где

Совершив преобразование запишем, что

Где А и — произвольные постоянные.

Теперь уже тело действительно совершает колебания — так называемые ЗатУХающие гармонические колебания. Если коэффициент сопротивления K=0, то мы получим:

Т. Е. обычное гармоническое колебание.

В том случае, когда , амплитуда колебания , в отличие от случая чисто гармонических колебаний, не есть постоянная величина, а зависит от времени; она стремится к нулю при . Следовательно, тело стремится к равновесию, но не монотонно, а колеблясь около положения равновесия, с постепенно — по экспоненциальному закону — затухающими размахами (Амплитудами). Как и для гармонических колебаний, величина называется Частотой, величина — периодом, а — Начальной фазой ЗаТухающего гармонического колебания. Величина называется АмплитУДой затухающего колебания. Логарифм амплитуды Убывает с постоянной скоростью K. Чтобы найти максимальное отклонение S, найдем производную S':

Приравнивая производную нулю, получим уравнение для определения экстремальных значений T:

Ясно, что максимумы и минимумы отклонений (с учетом знака) будут Чередоваться и следовать один за другим через полпериода

Отношение двух последовательных максимальных отклонеНИй будет равнО,

Постоянная величина называется Логарифмическим ДЕкрементом затухания.

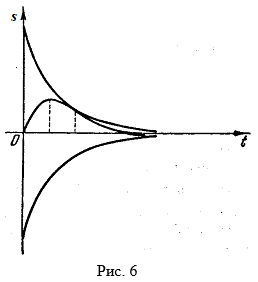
Схематический график затухающего гармонического колебания (при ) указан на рис. 6.

III. Исследование вынужденных колебаний. Резонанс. Обратимся теперь к вынужденным колебаниям, которые описываются линейным уравнением с правой частью

Рассмотрим практически наиболее важный случай, когда коэффициент сопротивления меньше коэффициента восстановления: и внешняя сила периодическая:

В силу свойств линейных неоднородных уравнений любое вынужденное колебание является результатом наложения собственного колебания системы и какого-нибудь наперед выбранного вынужденного колебания (см. П. I). Найдем частное вынужденное колебание, т. е. частное решение неоднородного уравнения

Пусть ; тогда не есть корень характеристического уравнения, и решение можно искать в виде . Находя известным способом коэффициенты А и В, придем к решению (необходимые выкладки рекомендуем провести читателю самостоятельно)

Где

и

Таким образом, Одно из вынужденных колебаний есть Простое гармоническое колебание с амплИТуДОй , частотой И начальной фазой . Всякое другое получается наложением этого собственное колебание системы:

Вследствие того, что первый член с возрастанием T довольно быстро стремится к нулю, через некоторое время движение будет описываться в основном только вторым членом. С этим связано интересное явление, возникающее при вынужденных колебаниях, так называемый резонанс.

Рассмотрим амплитуду вынужденного колебания и предположим, что величины K и W неизменны, т. Е. собственная частота системы постоянна. Выражение для запишем так:

Где , . Амплитуда пропорциональна величине

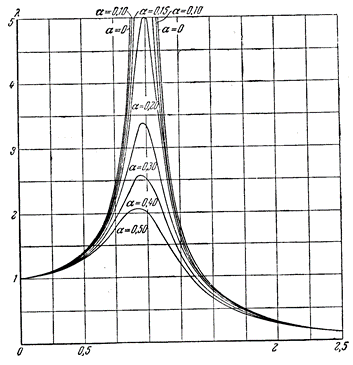
Характер изменения L при изменении Q виден на графиках функции , соответствующих различным значениям A. На рис. 7 даны графики при A = 0,50; 0,40; 0,30; 0,20; 0,15; 0,10; 0. Как правило, A — величина небольшая, ибо коэффициент сопротивления K составляет обычно малую долю коэффициента восстановления W.

Исследование показывает, что с увеличением Q, т. е. с увеличением возмущающей частоты величина L, а вместе с ней и амплитуда установившегося вынужденного колебания сначала возрастают до некоторого максимума, а затем быстро убывают, стремясь к нулю при . Этот максимум достигается при Т. е. при Легко проверить, что при этом амплитуда

При близости частоты возмущающей силы к величине и При малом K (это значит, что ) тело будет совершать через некоторый промежуток времени гармонические колебания с очень большой амплитудой, которая может быть совершенно несоразмерной с амплитудой синусоидальной силы, вызывающей само колебание системы. Это явление резкого возрастания амплитуды колебания под влиянием даже совсем малых внешнИХ воздействий и называется резонансом. Кривые на рис. 7 называются Кривыми резонанса.

Резонанс играет значительную роль в технике и физике. Каждое упругое тело (например, любое сооружение) имеет свою определенную собственную частоту колебания, зависящую только от свойств тела. Представим себе, что это тело под действием внешней силы выводится из состояния равновесия. Если частота внешней силы близка к собственной частоте, то воздействие силы, как бы мала она ни была, может оказаться огромным и разрушительным. При проектировании различных сооружений (машин, мостов, кораблей, самолетов и т. П.) особенно принимаются в расчет соображения о прочности, связанные с резонансом. Резонансом объясняется хорошо известное из опыта явление, когда небольшая «раскачка» упругого теЛА (скажем, моста) вызывает его поломку.

При отсутствии сопротивления, т. Е. когда K=0 (что на практике, однако, не может встретиться), амплитуда вынуждеННого колебания равна и обращается в бесконечность при совпадении возмущающей и собственной частот (см. рис. 7, кривая ). В том случае, когда , решение дифференциального уравнения колебания получается из общего решения, найденного выше, приданием K значения 0. Но если , то указанное решение не подходит, так как при ЭТом становится корнем характеристического уравнения . Решением, как было показано ранее, будет функция

Второй член (так называемый «вековой член») показывает, что с течением времени размахи колебания неограниченно возрастают, что здесь и иллюстрирует резонанс.

IV. Колебания в электрической цепи. КартиНУ, вполне аналогичную механическим колебаниям, представляют процессы, протекающие в электрической цепи, имеющей сопротивление R, самоиндукцию L, емкость С, причем в ней действует напряжение , Поступающее извне. Подобный вопрос мы уже рассматривали, в п. 1.4. где, однако, не принималась во внимание емкость. В общем случае необходимо учесть, что часть полного напряжения обусловливается наличием емкости. В физике показывается, что эта часть измеряется величиной где I — сила тока.

Таким образом, приходим к уравнению

Откуда дифференцированием по T получаем линейное уравнение второго порядка с постоянными коэффициентами

Это дифференциальное уравнение, описывающее явление течения тока, аналогично уравнению, описывающему явление механических колебаний.

Если внешняя электродвижущая сила постоянна (или вовсе отсутствует), то уравнение будет однородным. Ему соответствует ток, который в силу неравенства нулю сопротивления неизбежно будет затухающим. В электротехнике он называется переходным. Распространяя и дальше аналогию с механическими колебаниями, Можно сказать, что этот ток (при условии ) дает собственные колебания цепи (контура). Если существует внешнее возмущающее напряжение, такое, что не равно тождественно нулю, то неоднородное уравнение имеет частное решение: , которое дает вынужденный ток, называемый установившимся. Наконец, общее решение уравнения, т. е. зависимость силы тока от времени при любых условиях, получается сложением переходного и установившегося токов. Совершенно ясно, что, аналогично случаю механических колебаний, по прошествии некоторого промежутка времени переходный ток практически не будет влиять на течение электричества. В случае, когда (а следовательно, и ) есть синусоидальная функция времени, установившийся ток тоже будет синусоидальным. Здесь мы опять можем столкнуться с явлением резонанса, играющим особенно важную роль в колебательных контурах. В дальнейшие подробности входить нет нужды, так как с математической стороны ход явления подобен случаю механических колебаний.

< Предыдущая		Следующая >