21. Приложения к механике

I. Цепная линия.

Найдем форму гибкой нерастяжимой однородной нити (цепи), прикрепленной за два конца и находящейся под действием собственного веса (рис. 6).

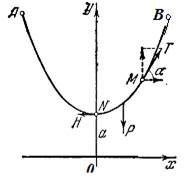
За ось Оу примем вертикальную прямую, проходящую через низшую точку N Линии; ось Ох проведем горизонтально, на неопределенном пока расстоянии от точки N.

Возьмем произвольную точку М линии. В условиях равновесия кусок нити NМ можно рассматривать как твердое тело. Оно подвержено действию трех сил: силы горизонтального натяжения Н, силы натяжения Т, приложенной в точке М и направленной по касательной к линии, и собственного веса Р, равного SD, где S — длина дуги NM, а D — Вес единицы длины нити.

Согласно условиям равновесия имеем:

Разделим почленно первое равенство на второе:

Следовательно, если есть искомое уравнение линии АNВ, то

где .

Продифференцируем это равенство по Х:

Будем решать это уравнение, как указано в П. 2.2, II. Положим , тогда , следовательно, получаем:

или

Откуда

В точке N имеем Х = 0 и должно быть (N — низшая точка линии). Значит, С1 = 0 и Перенося Z в правую часть и возводя в квадрат, приходим к равенству

.

Интегрируя, находим:

.

Выберем теперь расстояние ОN равным . Тогда С2 = 0, и мы получаем искомое уравнение линии

.

В этом примере наглядно видно, как, пользуясь начальными условиями задачи, удобно последовательно находить значения постоянных интегрирования. Предварительное составление общего решения привело бы к более громоздким выкладкам.

Обозначая через А, запишем:

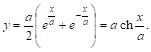
Это — уравнение цепной линии, которая потому так и названа, что ее форму, как мы видим, принимает свободно подвешенная цепь.

II. Задачи динамики материальной точки.

Пусть материальная точка движется прямолинейно под действием некоторой силы, направленной вдоль линии движения точки. Согласно второму закону Ньютона произведение массы на ускорение равно действующей силе: . Так как Где T — Время, а S — путь, то при отыскании закона движения мы приходим к дифференциальному уравнению второго порядка

В обычно встречающихся задачах сила F может зависеть от времени T, расстояния S и скорости движения т. е. .

В курсах механики принято производные по времени обозначать не штрихами, а точками: Поэтому дифференциальное уравнение движения примет вид

. (*)

Обычно задаваемые начальные условия и имеют ясный механический смысл: это начальное положение точки и ее начальная скорость. Рассмотрим теперь некоторые примеры.

1) Равномерно ускоренное движение.

Пусть сила F Постоянна; обозначим отношение Через А. Тогда . ИнтегриРуя, получим: и . Сразу видно, что и . Таким образом, мы получили хорошо известную формулу для пути при равномерно ускоренном движении: .

2) Движение точки в среде с сопротивлением.

Как показывает опыт, всякое тело испытывает при движении в среде сопротивление со стороны этой среды. Сила сопротивления возрастает со скоростью тела и зависит как от свойств среды (плотности, вязкости и т. д.), так и от размеров и формы движущегося тела. Если скорость движения невелика и тело имеет малые размеры, то силу сопротивления можно считать пропорциональной скорости N :

.

Коэффициент пропорциональности K > 0, а знак минус указывает, что сила сопротивления всегда направлена против движения. Если скорость движения велика, то сила сопротивления становится пропорциональной квадрату скорости, т. Е.

В этом случае коэффициент пропорциональности G рассчитывается по формуле

,

Где R — плотность среды, S — наибольшая площадь сечения тела, перпендикулярного к направлению движения (мИделево сечение), а С — Безразмерный коэффициент, определяемый опытным путем и зависящий от формы движущегося тела.

Разумеется, установить, в каком случае можно принять тот или иной закон сопротивления, можно только опытным путем.

В качестве примера рассмотрим падение тела на землю с учетом сопротивления воздуха.

Будем считать, что масса тела равна Т и начальная скорость его равна нулю. На тело действуют две силы: сила тяжести ТG и сила сопротивления, которую мы примем пропорциональной квадрату скорости движения. Дифференциальное уравнение примет вид

Применяя подстановку

Мы придем к уравнению первого порядка

Запишем его в виде

И введем обозначения: и Разделяя переменные, получим:

Или после интегрирования (см. формулу (11) таблицы интегралов)

Так как то . Тогда и

Из полученной формулы следует, что скорость N всегда меньше B И стремится к этому значению при . Таким образом, скорость вовсе не возрастает безгранично, как при свободном падении в безвоздушной среде, а стремится к определенному пределу — предельной скорости:

Практически предельная скорость достигается довольно быстро; величина предельной скорости (а также время ее наступления) увеличивается вместе с массой тела и с уменьшением коэффициента сопротивления G, что хорошо согласуется с наглядными представлЕНИЯми.

Перейдем теперь к установлению связи между скоростью падения и пройденным путем; для падения без учета сопротивления воздуха, как известно, , где S — путь, пройденный при падении. Для получения нужной зависимости можно было бы, зная скорость, интегрированием найти путь и потом искать связь между N И S. Мы, однако, поступим проще, исключив независимую переменную T из самого дифференциального уравнения. Для этого применим подстановку, указанную в п. 2.2., III:

ДИФференциальное уравнение с учетом введенных обозначений примет тогда вид

.

Разделяя переменные и интегрируя, получим:

Так как и, следовательно, , откуда . Заменяя A и B Их значениями, получим:

Из этой формулы следует, что если отношение велико (практически это значит, что тело плохо обтекаемо), то уже при небольших S величиной можно пренебречь, и мы приходим опять к пределенной скорости . Если же отношение очень мало, то, воспользовавшись приближенной формулой , верной для малых X, найдем, что при небольших S

,

Т. е. что приближенно верна формула для скорости при падении в безвоздушной среде.

Рекомендуем читателю самостоятельно проанализировать случай свободного падения тела при условии, что сила сопротивления пропорциоНАльна скорости, и убедиться, что и в этом случае скорость N имеет определенное предельное значение при возрастании T.

< Предыдущая		Следующая >