22. Дифференциальные уравнения высших порядков
Решение дифференциального уравнения становится более сложным по мере того, как в левую часть его начинают входить производные более высоких порядков. В этом пункте мы ограничимся только основными определениями, относящимися к уравнениям любого порядка.
Определение. Порядком дифференциального уравнения называют наивысший порядок производной, входяЩЕй в уравнение.
Обычно имеют дело с уравнениями, разрешенными относительно старшей производной. Тогда уравнение П-го порядка запишется в виде
![]() . (*)
. (*)
Общее рЕШение такого уравнения зависит от П произвольных постоянных: ![]() . Чтобы выделить частное решение, отвечающее конкретным условиям задачи, нужно задать НАчальные условия; они имеют следующий вид:
. Чтобы выделить частное решение, отвечающее конкретным условиям задачи, нужно задать НАчальные условия; они имеют следующий вид:
![]()
Т. е. при ![]() задаются значения самой функции и ее первых (N - 1) производных. Дифференцируя (П - 1) раз общее решение и подставляя начальные условия, мы получаем систему N уравнений с П неизвестными
задаются значения самой функции и ее первых (N - 1) производных. Дифференцируя (П - 1) раз общее решение и подставляя начальные условия, мы получаем систему N уравнений с П неизвестными ![]()
Вопрос о существовании и единственности частного решения, так же как в случаях П=1 и N=2, решается следующей теоремой:
Теорема существования и единственности решения. Если правая часть уравнения (*)— функция f — непрерывна вместе со своими частными производными по аргументам ![]() ПРи ЗНачениях
ПРи ЗНачениях ![]() , то уравнение имеет решение
, то уравнение имеет решение ![]() , и притом единственное, принимающее вместе со своими первыми
, и притом единственное, принимающее вместе со своими первыми ![]() производными при
производными при ![]() заданные значения:
заданные значения: ![]()
Укажем один тип уравнений П-го порядка, которые легко решаются при любом П, а именно:
![]()
Общее решение ЭТого уравнения мы получим, произведя последовательно N интегрирований; при каждом таком интегрировании будет появляться новая произвольная постоянная.
Пример. Решим уравнение ![]()
Имеем:
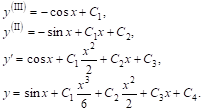
Изменяя обозначения произвольных постоянных, общее решение можно записать в виде
![]()
| < Предыдущая | Следующая > |
|---|