17. Уравнения в полных дифференциалах

Возьмем уравнение первого порядка, записанное в дифференциальной форме:

(A)

Определение. Если левая часть уравнЕНия (А) является полным дифференциалом некоторой функции и(Х,У), то это уравнение называется уравнением в полных дифференциалаХ.

Выражение же , есть полный Дифференциал, если (см. п. 3.9. раздела 3).

Найдем такую функцию И(Х, у), что

.

Тогда уравнение (А) можно записать так:

.

Последнее равенство означает, что между переменными Х и У существует зависимость вида

Где С — Произвольная постоянная. Полученная зависимость и дает общее решение уравнения (А). Следовательно, интегрирование уравнения (А) сводится к отысканию первообразной от левой части. Воспользовавшись выражениями для этой первообразной (найденными в п. 3.9. раздела 3), получаем общее решение уравнения (А) в виде

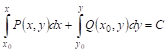
Или в виде

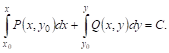
Пример. Найдем общее решение уравнения

.

Так как

То левая часть уравнения является полным дифференциалом некоторой функции И(Х, у). Беря за точку начало координат, имеем:

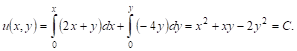
Решенное здесь дифференциальное уравнение является однородным, поэтому его можно проинтегрировать и способом, описанным в п. 1.4.

< Предыдущая		Следующая >