16. Однородные и линейные уравнения первого порядка

Прежде всего, рассмотрим простые и важные классы уравнений первого порядка, приводящихся к уравнениям с разделяющимися переменными.

I. Однородные уравнения.

Определение. Уравнение

Называется однородным, если функция может быть представлена как функция отношения своих аргументоВ:

Например, уравнение

Однородное, так как его можно записать в виде

В общем случае переменные в однородном уравнении не разделяются. Однако, вводя вспомогательную неизвестную функцию U по формуле

или

Мы сможем преобразовать однородное уравнение в уравнение с разделяющимися переменными.

Действительно, имеем:

И уравнение прИНимает вид

, т. е.

Отсюда

После интегрирования получаем:

Найдя отсюда выражение для И как функции от Х, и возвращаясь к переменной , получим искомое решение однородного уравнения.

Чаще всего не удается просто найти явное выражение для И. Тогда после интегрирования следует в левую часть вместо U ПодстаВить ; в результате мы получим решение уравнения в неявном виде.

Разумеется, мы предполагаем, что . Если , то и не нужно делать никаких преобразований, ибо само заданное уравнение - с разделяющимися переменными.

Нет необходимости запоминать полученные выше формулы: в каждом примере нетрудно проделать полностью указанное преобразование.

Пример. Найдем решение однородного уравнения

Замена приводит к уравнению

или

Разделяя переменные, находим:

Откуда

, или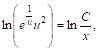

И значит,

Возвращаясь к перемеННой У, приходим к общему решению:

II. Линейные уравнения. Вторым часто встречающимся типом уравнений первого порядка явлЯЕтся линейное уравнение.

Определение. Уравнение вида

(*)

Т. Е. линейное относительно искомой фуНКции и ее производНОй, называется линейным.

Здесь Р(Х) и Q(Х) — известные функции независимой переменной Х.

Уравнение (*) сводится к двум уравнениям с разделяющимися переменными путем следующего искусственного приема. Запишем функцию У в виде произведения двух функций: . одной из них мы можем распорядиться совершенно произвольно; при этом вторая должна быть определена в зависимости от первой таким образом, чтобы их произведение удовлетворяло данному линейному уравнению. Свободой выбора одной иЗ функций U и N мы воспользуемся для максимального упрощения уравнения, получающегося после замены.

Из равенства находим производную У':

Подставляя это выражение в уравнение (*), имеем:

, или .

Выберем в качестве N какое-нибудь частное решение уравнения

. (**)

Тогда для отыскания U получим уравнение

. (***)

Сначала найдем N из уравнения (**). Разделяя переменные, имеем:

Откуда

и .

Как и раньше, под неопределенным интегралом здесь понимается Какая-нибудь одна первообразная от функции Р(Х), т. е. N является вполне определенной функцией от Х.

Зная N, находим далее И из уравнения (***):

И значит,

Здесь мы уже берем для U все первообразные. По И и N найдем искомую функцию У:

Полученная формула дает общее решение линейного уравнения (*).

Положение не изменится, если мы прибавим произвольную постоянную к интегралу в показателе. В самом деле, эта вторая произвольная постоянная в конечном счете исчезнет, так как один множитель будет содержать ее в знаменателе, а другой — в числителе.

Можно решать задачу с помощью определенных интегралов с переменным верхним пределом. При этом

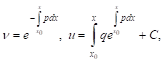
Частное решение, соответствующее начальному условию , Получается отсюда при .

Как и раньше, мы не настаиваем на запоминании общей формулы. Следует помнить лишь способ решения и применять его в каждом конкретном случае.

Пример. Решим уравнение

Положим , тогда . Имеем: или Пусть . Отсюда и, значит, Т. е. Следовательно, откуда и, значит, Имеем окончательно:

.

Рассмотрим одну важную задачу электротехники, которая приведет нас к линейному дифференциальному уравнению первого порядка. Пусть ЭЛектрическая цепь имеет сопротивление R и самоиндукцию L.

Если через I обозначить силу тока в цепи, а через Е электродвижущую силу, то, как известно из физики,

.

Считая, что Е является известной функцией времени, получаем линейное уравнение, которое запишем в виде

Проинтегрируем это уравнение в предположении, что при начальном условии . Это означает, что мы включаем в цепь, в которой не было тока, постоянную электродвижущую силу. Воспользовавшись общей формулой, выраженной при помощи определенных интегралов, получим:

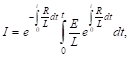
Или, выполняя интегрирование,

.

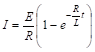Ток I слагается как бы из двух токов: тока , соответствующего закону Ома, и экстратока замыкания , протекающего в обратном направлении. Экстраток замыкания быстро стремится к нулю, и поэтому в цепи довольно скоро устанавливается постоянный ток. Еще проще решается задача о размыкании цепи. В этом случае мы считаем, что и . Тогда получается уравнение с разделяющимися переменными Решая его, ПолуЧиМ - экстраток размыкания. Скорость СтремЛения экстратока к нулю зависит от отношения : чем это отношение больше, тем быстрее экстраток затухает.

Рекомендуем читателю самостоятельно решить задачу в случае, когда электродвижущая сила Е синусоидальна, т. е. когда .

< Предыдущая		Следующая >