15. Некоторые задачи физики

Хотя дифференциальные уравнения с разделяющимися переменными являются весьма частными случаями уравнений первого порядка, к ним приводят многие различные задачи из области физики и механики.

Заметим сразу же, что при решении задач физического характера, приводящих к дифференциальным уравнениям, основную трудность представляет, как правило, составление самих дифференциальных уравнений. Здесь нет общего метода, и каждая задача требует своего подхода, основанного на знании соответствующего закона физики. Рассмотрим некоторые из этих задач, чтобы показать на примерах, как составляются дифференциальные уравнения. Приведенные примеры помогут читателю уяснить суть дела и перейти к самостоятельному решению подобных задач.

1) Радиоактивный распад. Экспериментальным путем установлено, что Скорость радиоактивного распада пропорциональна количеству нераспавшегося вещества. Считая, что начальное количество вещества равно , найдем зависимость между количеством нераспавшегося вещества М и временем T.

Скорость радиоактивного распада равна производной от количества вещества М по времени T, т. е. . Но по условию

Где K — коэффициент пропорциональности. Знак минус берется потому, что с возрастанием T количество вещества М уменьшается. Обращаем внимание читателя на то, что в дифференциальное уравнение не входит величина ; она войдет в начальное условие, которое имеет вид . Разделим переменные в полученном уравнении:

Интегрируя, получим:

Откуда

Из начального условИЯ следует, что . Следовательно, частное решение, отвечающее условиям задачи, имеет вид

Константу K можно определить экспериментально, установив количество нераспавшегося вещества в какой-то момент времени. Пусть, например, половина начального количества Г распадется в течение 26,7 минуты. Здесь при T=26,7 М = 0,5. Поэтому , откуда . Следовательно, процесс распада протекает по формуле

Для того чтобы узнать, какое количество вещества осталось нераспавшимся, например, через 10 минут после начала опыта, достаточно в эту формулу подставить T=10:

2) Охлаждение тела. Согласно закону, установленному Ньютоном, Скорость охлаждения тела пропорциональна разности междУ Температурой тела и температурой окружающей среды.

Пусть тело нагрето до температуры ; температуру окружающей среды будем считать постоянной и равной . Найдем зависимость между изменяющейся температурой Т тела и временем охлаждения T.

Пусть в момент времени T температура тела равна Т. Скорость изменения температуры, т. Е. , по закону Ньютона пропорциональна разности ; следовательно,

Знак минус выбран потому, что с возрастанием T температура T тела уменьшается. Коэффициент пропорциональности K зависит как от физических свойств тела, так и от его геометрической формы (ясно, что скорость охлаждения раскатанного листа стали больше, чем первоначального стального слитка).

Разделяя переменные, получим . Отсюда

и .

Подставляя начальное условие , найдем С: , т. Е. . Окончательно закон охлаждения имеет вид

Коэффициент пропорциональности K должен быть либо задан, либо установлен экспериментально путем измерения температуры T в некоторый момент времени T. Отметим, что теоретически температура тела сравняется с температурой окружающей среды лиШЬ при .

В обоих приведенных примерах Соответствующий физический закон непосредственно устанавливает связь между производной неизвестной функции и самой функцией (независимая переменная T в уравнение не входит).

Рассмотрим теперь более сложный пример.

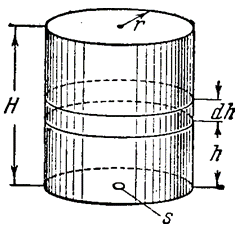
3) Истечение жидкости из цилИНдра. Цилиндрический сосуд, в дне которого имеется отверстие, наполнен жидкостью. Найдем время Т, в течение которого жидкость вытечет из сосуда, если высота столба жидкости равна Н, радиус цилиндра равен R, площадь отверстия равна S (рис. 3).

При решении задачи используем закон ТоРичеллИ.

Скорость N истечения жидкости в случае отверсТИй, небольших сравнительно с высотой столба жидкости, равна , где H — высота уровня жидкости над отверстием, а g — ускорение силы тяжести. (Эта скорость равна скорости при свободном падении тела с высоты H.)

Если бы убыль жидкости постоянно возмещалась, то скорость истечения по закону Торичелли оставалась бы постоянной, и тогда имевшееся вначале количество жидкости вытекло бы за Сек.

Но без такого возмещения уровень жидкости все время понижается, и скорость истечения уменьшается; задача оказывается более сложной.

Пусть в момент времени T высота жидкости в цилиндре равна H (рис. 3). Мы найдем связь между Dt и Dh, если предположим, что за бесконечно малый промежуток времени Dt скорость истечения будет постоянной и равной . Тогда объем DV жидкости, вытекающей из цилиндра за время Dt, будет равен объему цилиндра с основанием S и высотой :