14. Уравнения с разделяющимися переменными

Рассмотрим уравнение вида

(*)

Где и — заданные функции. В этом дифференциальном уравнении переменные разделены, т. Е. каждая из переменных содержится только в той части уравнения, где находится ее дифференциал. Уравнение является частным случаем рассматриваемого уравнения.

В обеих частях уравнения (*) стоят дифференциалы некоторых функций; справа этот дифференциал выражен прямо через независимую переменную Х, а слева через промежуточный аргумент У, который является функцией от Х. Именно эта зависимость У от Х И является искомой. Произведя интегрирование, мы получим связь между переменными Х и У, освобожденную от их дифференциалов:

Если задано начальное условие , то, определяя постоянную С, получим частное решение, удовлетворяющее данному условию. Воспользовавшись определенными интегралами, можно сразу записать искомое частное решение:

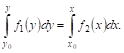
При этом значения и действительно соответствуют друг другу, так как обе части равенства обращаются в нуль при замене верхних пределов У и Х на и .

Выполняя фактически интегрирование, мы обычно получаем неизвестную функцию У в неявном виде.

Пример. Найдем решение уравнения

Удовлетворяющее условию

Выполняя интегрирование, получим:

или

Для удобства потенцирования мы записали произвольную постоянную в виде . Подставляя в общее решение начальное условие, найдем С:

Т. е.

Таким образом, функция Является искомым частным решением данного уравнения. Если бы мы воспользовались определенными интегралами, то получили бы

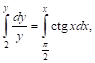
Т. е.

или

Потенцируя, приходим к тому же частному решению

Очень часто встречаются уравнения, в которых переменные еще не разделены, но их можно разделить, производя простые арифметические операции.

Определение. Дифференциальные уравнения, в которых переменные можно разделить посредством умножения обеих частей уравнения на одно и то же выражение, называются дифференЦИальными уравнениями с разделяющимися переменными.

Таким будет, например, уравнение

В нем переменные еще не разделены, однако, умножив обе его части на , мы приходим к уравнению с разделенными переменными. Легко также разделить переменные, если уравнение записано в дифференциальной форме и имеет вид

Деля обе части уравнения на произведение , получим:

Нам теперь даже не обязательно переносить одно из слагаемых в правую часть. Интегрируя, запишем:

Пример. Найдем общее решение уравнения

Разделяя переменные, приведем его к виду

Интегрируя, получим:

Т. е.

Итак, мы нашли общее решение, причем У является неявной функцией от Х.

Предоставляем читателю проверить, что, заменяя С на , мы можем представить решение в таком виде:

< Предыдущая		Следующая >