13. Дифференциальные уравнения первого порядка

При изучении интегрального исчисления функций одной переменной мы сталкивались с необходимостью отыскивать неизвестную функцию У По ее производной или дифференциалу.

Уравнение

(*)

Где У — Неизвестная функция от Х, — Заданная функция, является простейшим Дифференциальным уравнением. Для его решения, т. е. для отыскания неизвестной функции У, нужно проинтегрировать данную функцию . При этом, как известно, мы получим бесчисленное множество функций, каждая из которых будет удовлетворять условию (*). В этой главе нам удобнее будет под интегралом понимать какую-либо одну первообразную. Тогда любое решение уравнения (*) запишется в виде

Вскоре мы увидим, что гораздо чаще нам приходится иметь дело с уравнениями более сложного вида. Именно в эти уравнения, помимо производной У' и независимой переменной Х, может входить и сама неизвестная функция У. Примером тому служат уравнения

и т. д.

Заменяя У' на , можно эти самые уравнения переписать в дифференциальной форме:

Определение. Дифференциальным уравнением первого порядка называется уравнение, связывающее независимую переменную, неизвестную функцию и ее производную.

Так как производную можно представить в виде отношения дифференциалов, то уравнение может содержать не производную, а дифференциалы неизвестной функции и независимой переменной.

Мы будем рассматривать только такие уравнения, в которых неизвестная функция зависит от одного аргумента.

Дифференциальное уравнение первого порядка в общем виде записывается так:

В частных случаях в левую часть уравнения могут не входить Х или У, но всегда обязательно входит У'. Нам придется в основном иметь дело с уравнениями, разрешенными относительно производной, т. е. вида

Определение. Решением дифференциального уравнения называется всякая функция, обращающая уравнение в тождество при подстановке в него этой функции и ее производной взамен неизвестной функции и ее производной.

Простейшие примеры показывают, что дифференциальное уравнение может иметь бесчисленное множество решений. Мы наблюдали это уже на примере уравнения (*). Простой проверкой легко убедиться также, что уравнение имеет решениями функции , а уравнение функции , где С — Любое число.

Уравнение имеет решениями функции .

В самом деле, найдя производную и подставив ее в уравнение, получим тождество

Как мы видим, в решения приведенных дифференциальных уравнений входит Произвольная постоянная С; придавая ей различные значения, мы будем получать разные решения.

Несмотря на то, что рассмотренные примеры носят частный характер, мы все-таки, не приводя доказательства, сделаем следующий общий вывод:

Любое дифференциальное уравнение имеет бесчисленное множество решений, которые определяются формулой, содержащей одну произвольную постоянную. Эту совокупность решений будем записывать так:

.

Определение. Общим решением дифференциального уравнения первого порядка называется совокупность его решений, определяемая формулой , где С — произвольная постоянная.

Придавая произвольной постоянной С определенные числовые значения, мы будем получать Частные решения.

В дальнейшем при решении конкретных задач нас будут интересовать преимущественно частные решения. Необходимо выяснить, каким же образом из общего решения можно выделить требуемое решение. Зададим для этого начальное условие. Задать начальное условие дифференциального уравнения первого порядка это значит указать пару соответствующих друг другу значений независимой переменной и функции. Записывают это так:

.

Покажем на примере, как по общему решению и заданному начальному условию можно отыскивать соответствующее этому условию частное решение.

Выше мы видели, что уравнение имеет общее решение . Зададим начальное условие . Подставив эти значения Х и У В общее решение, найдем С: 6 = 2С, откуда С = 3. Следовательно, функция У = 3Х удовлетворяет как дифференциальному уравнению, так и начальному условию.

Вопрос о том, в каком случае можно утверждать, что частное решение дифференциального уравнения, удовлетворяющее данному начальному условию, существует, а также что оно будет единственным, выясняется теоремой, которую мы приведем без доказательства.

Теорема существования и единственности решения. Если функция непрерывна в области, содержащей точку , то существует решение уравнения такое, что У обращается в при .

Если, кроме того, непрерывна также и частная производная , то это решение уравнения единственно.

Перейдем теперь к геометрической иллюстрации введенных понятий.

График любого частного решения дифференциального уравнения называется Интегральной кривой. Общему решению соответствует Семейство интегральных кривых. Так как мы уже проверили, что уравнение имеет общее решение , то соответствующее ему семейство интегральных кривых — пучок прямых, проходящих через начало координат

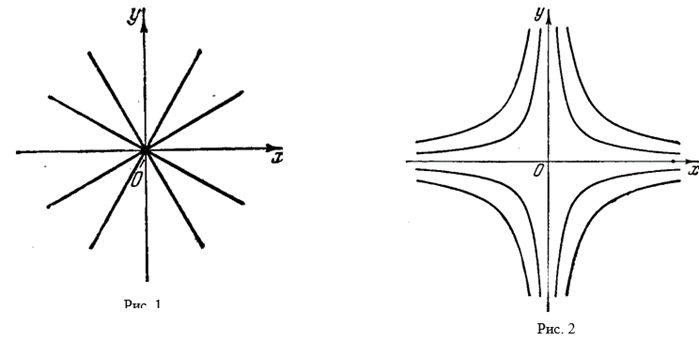(рис. 1). Уравнение имеет общее решение . Ему соответствует семейство равнобочных гипербол, асимптотами которых являются оси координат (рис. 2), а также прямая У = 0.

Задание начального условия , означает задание точки , через которую должна проходить интегральная кривая, соответствующая искомому частному решению. Таким образом, отыскание частного решения по начальному условию геометрически означает, что из семейства интегральных кривых мы выбираем ту, которая проходит через точку . Согласно теореме существования и единственности решения через каждую точку, в которой функции и непрерывны, проходит одна-единственная интегральная кривая. Если в данной точке эти условия нарушены, то это означает, что через эту точку либо вообще не проходит ни одна интегральная кривая, либо проходит несколько. Возьмем, например, уравнение . Из рис. 1 видно, что через начало КоОрдинат проходит бесчисленное множество его интегральных кривых. Это не противоречит теореме, так как в точке (0, 0) условия теоремы существования нарушены: правая часть уравнения становится неопределенной. В дальнейшем всегда предполагается, что если мы отыскиваем частное решение уравнения по заданным начальным условиям , то в точке выполняются условия теоремы существования и единственности. Такие начальные условия будем называть Возможными.

Теперь мы можем уточнить определение общего решения:

Общее решение дифференциального уравнения обладает тем свойством, что из него по любому заданному возможному начальному условию может быть найдено частное решение, удовлетворяющее этому условию.

Это означает, что, подставляя в общее решение значения и , мы получаем уравнение относительно С: , из которого всегда может быть найдено одно-единственное значение . Функция и будет искомым частным решением.

Отметим еще, что отыскание решения дифференциального уравнения часто называют интегрированием уравнения.

Перейдем теперь к приемам решения отдельных типов дифференциальных уравнений.

< Предыдущая		Следующая >