12. Непротиворечивость евклидовой планиметрии
«Точкой» будем называть любую упорядоченную пару вещественных чисел (Х, у), при этом числа Х, у будем называть координатами «точки». «Прямой» назовем множество всех «точек», координаты которых удовлетворяют линейному уравнению
![]() (3)
(3)
![]() . Это уравнение будем называть уравнением «прямой». «Прямые» Х= 0, У = 0 будем называть осями координат, а «точку» (0,0) — началом координат. Если «точка» является одной из точек «прямой», будем говорить, что «точка» принадлежит «прямой». Не определяя пока других основных понятий, покажем, что аксиомы I.1 - I.3 выполнены. Чтобы не загромождать текст, кавычки в словах «точка» и «прямая» опустим.
. Это уравнение будем называть уравнением «прямой». «Прямые» Х= 0, У = 0 будем называть осями координат, а «точку» (0,0) — началом координат. Если «точка» является одной из точек «прямой», будем говорить, что «точка» принадлежит «прямой». Не определяя пока других основных понятий, покажем, что аксиомы I.1 - I.3 выполнены. Чтобы не загромождать текст, кавычки в словах «точка» и «прямая» опустим.
Аксиома I.1 выполнена, поскольку уравнение (3) имеет бесконечно много решений (Х, у). Справедливость аксиомы I.2 следует из того, что три точки (0, 0), (1, 0) и (0, 1) не могут являться точками никакой прямой. Действительно, если бы они являлись точками некоторой прямой (3), то была бы выполнена система
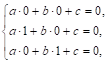
Откуда получили бы А = B = с = 0, что противоречит условию ![]() . Покажем, что выполнена и аксиома I.3. Пусть
. Покажем, что выполнена и аксиома I.3. Пусть ![]() и
и ![]() — данные различные точки. Рассмотрим прямую (3), положив
— данные различные точки. Рассмотрим прямую (3), положив ![]() ,
, ![]() ,
, ![]() Уравнение (3) можно при этом записать в виде
Уравнение (3) можно при этом записать в виде ![]() Тогда
Тогда
![]()
И
![]()
Следовательно, точки ![]() и
и ![]() принадлежат прямой Ах + Bу + С = 0. Покажем, что эта прямая единственна. Предположим, что есть еще прямая
принадлежат прямой Ах + Bу + С = 0. Покажем, что эта прямая единственна. Предположим, что есть еще прямая ![]() содержащая точки
содержащая точки ![]() и
и ![]() . Тогда система двух линейных уравнений
. Тогда система двух линейных уравнений
![]() и
и ![]()
Имеет два различных решения ![]() и
и ![]() , откуда следует, что уравнения линейно зависимы, т. Е. отличаются множителем. Но это означает, что прямые совпадают.
, откуда следует, что уравнения линейно зависимы, т. Е. отличаются множителем. Но это означает, что прямые совпадают.
Осталось убедиться, что в строящейся нами модели ВыПолняется аксиома параллельных Евклида. Пусть даны точка ![]() и прямая L, уравнение которой
и прямая L, уравнение которой
![]()
Так как ![]() , то
, то ![]() Рассмотрим прямую L', Заданную уравнением
Рассмотрим прямую L', Заданную уравнением ![]() , проходящую через точку A не имеющую с прямой L общих точек. Ясно, что коэффициенты
, проходящую через точку A не имеющую с прямой L общих точек. Ясно, что коэффициенты ![]() должны удовлетворять двум условиям:
должны удовлетворять двум условиям:
Во-первых,
![]() (4)
(4)
И, во-вторых, система
![]() (5)
(5)
Должна быть несовместной. Условие несовместности означает, что ![]() и
и ![]() , где M — некоторое число, отличное от нуля. Из (4)
, где M — некоторое число, отличное от нуля. Из (4) ![]() . Следовательно,
. Следовательно, ![]() , т. е. прямая L' единственна.
, т. е. прямая L' единственна.
Таким образом, построена модель планиметрии Евклида. Все ее понятия реализованы в терминах арифметики вещественных чисел. Поэтому построенная модель называется Арифметической. Ясно, что эта модель системы аксиом планиметрии Евклида решает вопрос о непротиворечивости планиметрии Евклида. Действительно, если бы в планиметрии Евклида существовали два взаимно исключающих друг друга утверждения, то, пересказанные в терминах модели, они явились бы противоречащими друг другу утверждениями арифметики веЩЕственных чисел.
Таким образом, как и в случае геометрии Лобачевского, мы доказали Условную нЕПротиворечивость планиметрии Евклида. Но при этом с помощью арифметической модели вопрос о непротиворечивости планиметрии Евклида (а стало быть, и планиметрии Лобачевского) выведен за рамки геометрии.
| < Предыдущая | Следующая > |
|---|