10. Непротиворечивость планиметрии Лобачевского

Как уже отмечалось, геометрия Лобачевского возникла в результате попыток доказать от противного утверждение V постулата Евклида. Его логическое отрицание не привело к противоречию с остальными аксиомами, появилась непривычная с точки зрения наглядных представлений, но содержательная и логически стройная геометрия, внутри которой не удалось получить двух взаимно исключающих утверждений. Однако отсутствие противоречий еще не означает, что они не могут появиться при дальнейшем развитии геометрии Лобачевского. Естественно возникает проблема, как доказать непротиворечивость этой геометрии, т. Е. отсутствие в ней двух утверждений, логически отрицающих друг друга.

Решить вопрос о непротиворечивости геометрии Лобачевского позволяет построение так называемой Модели, или, как еще говорят, Интерпретации, реализации. Мы рассмотрим здесь только планиметрию Лобачевского. В аксиоматике планиметрии Лобачевского основными понятиями являются «точка», «прямая», отношение порядка, выражаемое словами «лежать между» для точек одной прямой и «расстояние между точками».

Построение модели начинается с того, что эти основные понятия определяются через некоторые понятия планиметрии Евклида (реализуются в терминах планиметрии Евклида). Поскольку все понятия планиметрии Лобачевского можно определить через основные, то каждое понятие определяется при этом через соответствующие понятия евклидовой планиметрии. Если при таком определении основных понятий все аксиомы планиметрии Лобачевского, сформулированные в терминах евклидовой планиметрии, оказываются верными утверждениями последней, то говорят, что построена модель планиметрии Лобачевского на плоскости Евклида (реализация, интерпретация).

Так как все теоремы планиметрии Лобачевского являются логическими следствиями только аксиом, то все они справедливы в построенной модели, при этом каждая теорема формулируется в терминах евклидовой планиметрии и является в ней теоремой.

Отсюда ясно, что Модель решает вопрос о непротиворечивости. В самом деле, если бы в планиметрии Лобачевского Были два утверждения, логически противоречащие друг другу, то, пересказанные в терминах модели, они были бы противоречивыми утверждениями евклидовой планиметрии. В таком случае оказалась бы противоречивой евклидова планиметрия.

Таким образом, Построение модели решает вопрос о непротиворечивости планиметрии Лобачевского условно (со ссылкой на непротиворечивость геометрии Евклида). Что касается вопроса о непротиворечивости геометрии Евклида, то он, во-первых, не стоит так остро хотя бы потому, что евклидова геометрия, имея опытное происхождение, проверена тысячелетним человеческим опытом, а во-вторых, он также может быть решен построением соответствующей модели.

Покажем, как решается вопрос о непротиворечивости планиметрии Лобачевского на примере модели Пуанкаре.

Рассмотрим на евклидовой плоскости открытую полуплоскость Л, ограниченную прямой Х (будем считать ее горизонтальной). Назовем Л верхней полуплоскостью, а ее границу — Х — Абсолютом.

Точками плоскости Лобачевского будем называть точки верхней полуплоскости, а Прямыми — открытые полуокружности верхней полуплоскости с концами на абсолюте (значит, их центры лежат на Х) и лучи этой полуплоскости с началом на Х, перпендикулярные прямой Х. Эти полуокружности и лучи будем называть также Неевклидовыми прямыми.

Отношение «лежать между» на неевклидовой прямой отвечает отношению «лежать между» для точек евклидовых полуокружностей и лучей в обычном смысле.

Наконец, определим «расстояние между точками». Оно определяется по-разному в зависимости от того, расположена точка на полуокружности или на луче.

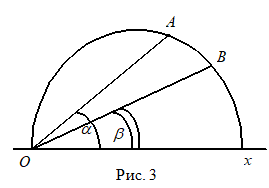
Если точки А и В лежат на полуокружности (рис. 3), то ВыбеРем один из концов О этой полуокружности и Неевклидовым расстоянием между точками А и В назовем

(1)

Где С — некоторое положительное число, A и B — углы, образованные соответственно лучами ОА и OВ с абсолютом.

Если же точки А и В лежат на вертикальном луче с началом , то неевклидовым расстоянием между ними назовем

(2)

Теперь нужно убедиться, что при указанном определении основных понятий планиметрии Лобачевского выполняются все ее аксиомы, сформулированные в новых терминах.

Аксиома I.1. Всякая неевклидова прямая содержит по крайней мере две точки верхней полуплоскости.

Справедливость утверждения очевидна, поскольку и полуокружность и луч содержат бесконечное множество точек.

Аксиома I.2. Существуют по крайней мере три точки верхней полуплоскости, не лежащие на одной неевклидовой прямой.

Это утверждение справедливо, поскольку, например, три точки, лежащие на невертикальном отрезке верхней полуплоскости, не могут принадлежать одной неевклидовой прямой.

Аксиома I.3. Через любые две точки верхней полуплоскости проходит неевклидова прямая и притом только одна.

Проведем через данные точки А и В верхней полуплоскости прямую АВ (евклидову). Если , то А И В лежат на вертикальном луче, т. е. на неевклидовой прямой. При этом ясно, что через них не проходит ни одна полуокружность с центром на абсолюте. Если АВ не перпендикулярна абсолюту, то проведем серединный перпендикуляр к отрезку АВ. Он пересекает абсолют в некоторой точке О. Полуокружность с центром О, проходящая через А и В, есть единственная неевклидова прямая, проходящая через эти точки.

Наконец, покажем, что ВыполНена аксиома VЛ существуют Такие неевклидова прямая р и не лежащая на ней точка А верхней полуплоскости, что через А проходят по крайней мере две НеевКлидовы прямые, не пересекающие прямую р.

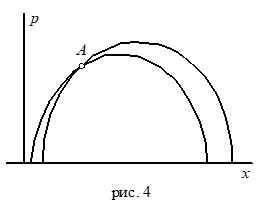
Проведем какой-нибудь луч Р с началом на абсолюте и перпендикулярный абсолюту. Возьмем произвольную точку А Верхней полуплоскости, не лежащую на Р. Ясно, что через точку А проходит бесконечно много полуокружностей с центрами на абсолюте, не пересекающих луч Р (рис. 4). Аксиома VЛ Выполнена.

Таким образом, мы установили, что При определении основных понятий планиметрии Лобачевского указанным выше образом выполняются все ее аксиомы. Следовательно, Построена модель планиметрии Лобачевского в терминах евклидовой планиметрии. Эта модель была построена Пуанкаре.

Как мы уже отмечали, построение модели решает вопрос о непротиворечивости системы аксиом планиметрии Лобачевского условно: планиметрия Лобачевского непротиворечива постольку, поскольку непротиворечива планиметрия Евклида. В силу важности вывода повторим аргументацию еще раз, имея в виду уже построенную модель Пуанкаре.

Предположим, что в планиметрии Лобачевского имеют место две противоречащие одна другой теоремы. Пользуясь моделью Пуанкаре, мы можем сформулировать эти теоремы в терминах евклидовой геометрии. Получим два исключающих друг друга утверждения в евклидовой геометрии, т. Е. получим противоречие в геометрии Евклида.

Как уже отмечалось, геометрия Лобачевского возникла при решении вопроса о независимости V постулата Евклида. Доказательство логической непротиворечивости планиметрии Лобачевского решает вопрос об этом. В самом деле, предположим, что аксиома параллельных Евклида V (она эквивалентна V постулату) является следствием остальных аксиом евклидовой геометрии, т. е. аксиом первых четырех групп I - IV. Поскольку аксиоматика планиметрии Лобачевского включает в себя эти четыре группы аксиом, то утверждение аксиомы параллельных Евклида было бы справеДЛиво в планиметрии Лобачевского. Но это противоречило бы аксиоме VЛ. Т. Е. система аксиом планиметрии Лобачевского была бы противоречивой.

Многие задачи геометрии Лобачевского проще решать в модели Пуанкаре, поскольку она построена на основе хорошо известной геометрии Евклида. В частности, в модели удобно выводить различные формулы геометрии Лобачевского.

< Предыдущая		Следующая >