06. Попытки доказательства V постулата. Геометрия Н. И. Лобачевского

История математики накопила много «доказательств» V постулата, но все они были ошибочными, причем содержали логическую ошибку одного плана: доказательство этого постулата основывалось на утверждении, которое казалось наглядно очевидным, а вместе с тем было равносильным V постулату. Таких равносильных данному постулату утверждений (эквивалентов) накопилось много.

1. Через точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.

2. Две параллельные прямые при пересечении их третьей прямой образуют равные соответственные или внутренние накрест лежащие углы.

3. Сумма углов треугольника равна 180°.

4. Множество точек, лежащих по одну сторону от данной прямой на одном и том же расстоянии от нее, есть прямая.

5. Существуют подобные неравные треугольники.

Следует отметить, что хотя попытки доказать V постулат и не привели к ожидаемому результату, эти исследования сыграли важную роль в развитии геометрии, поскольку в них прослеживалась система далеко идущих следствий, вытекающих из V постулата или предложения, ему эквивалентного. Проблема V постулата «обросла» большим количеством информации и была одной из самых популярных в геометрии вплоть до XIX в.

Заметный след в проблеме V постулата оставили работы итальянского математика Д. Саккери (1667-1733 гг.), немецкого математика и физика Г. Ламберта (1728-1777 гг.) и выдающегося французского математика А. Лежандра (1752-1833 гг.). В работе Саккери «Евклид, очищенный от всех родИмых пятен», вышедшей в 1733 г., делается попытка доказать V постулат методом от противного. В основе рассуждении Саккери лежит четырехугольник с двумя прямыми углами при основании и равными боковыми сторонами. Относительно двух других углов этого четырехугольника могут быть три гипотезы: углы прямые, тупые или острые. Саккери доказывает, что гипотеза прямого угла эквивалентна V постулату, т. Е., приняв V постулат, мы можем доказать гипотезу прямого угла и, обратно, приняв В Качестве аксиомы гипотезу прямого угла, можем доказать V постулат.

Гипотеза тупого угла приводит к противоречию и, значит, должна быть отвергнута. Приняв гипотезу острого угла, Саккери получает ряд следствий, противоречащих привычным геометрическим представлениям. Однако Саккери понимает, что нельзя отвергнуть гипотезу острого угла только на том основании, что основанные на ней выводы приводят к утверждениям, противоречащим наглядным представлениям, и ищет логическое противоречие. Такое логическое противоречие, как ему кажется, он находит, однако оно оказывается следствием вычислительной ошибки.

В сочинении Ламберта «Теория параллельных линий», изданном в 1766 г., в основу положен четырехугольник с тремя прямыми углами. Относительно четвертого угла высказываются три гипотезы: этот угол прямой, тупой или острый. Ламберт Устанавливает, что гипотеза прямого угла эквивалентна V постулату, гипотеза тупого угла противоречит остальным аксиомам геометрии. Приняв гипотезу острого угла, он развивает на ее основании целую систему далеко идущих следствий, многие из которых противоречат наглядным представлениям о свойствах прямых. Однако Ламберт, как Саккери, ищет логическое противоречие. В отличие от Саккери он не сделал ошибки, в результате которой можно было бы отвергнуть гипотезу острого угла. Напротив, в своем сочинении Ламберт пишет: «Доказательство евклидова постулата может быть доведено столь далеко, что остается, по-видимому, ничтожная мелочь. Но при тщательном анализе оказывается, что в этой кажущейся мелочи и заключается вся суть вопроса; обыкновенно она содержит либо доказываемое предложение, либо равносильный ему постулат». Среди геометров XVIII в. Ламберт ближе всех стоял к верному решению проблемы V постулата.

Так же как Саккери и Ламберт, Лежандр пытается доказать утверждение V постулата методом от противного. За основу своих рассуждений Лежандр выбирает эквивалентное V постулату утверждение о том, что сумма углов треугольника равна 180°, и рассматривает три гипотезы: сумма углов треугольника больше 180°, равна 180° и меньше 180°. Первая гипотеза отвергается, поскольку противоречит остальным аксиомам геометрии. Вторая гипотеза эквивалентна V постулату. Отвергнуть третью гипотезу Лежандру не удалось.

Таким образом, XVIII в. не принес решения проблемы V постулата. Но уже в 20-х годах XIX в. эта труднейшая проблема геометрии была решена.

Первым это сделал профессор Казанского университета Николай Иванович Лобачевский (1792—1856). В своем докладе на заседании Ученого совета физико-математического факультета в феврале 1826 г. Лобачевский отчетливо формулирует положение о том, что V постулат не может быть выведен из остальных аксиом геометрии Евклида. Подобно Саккери, Ламберту и Лежандру, Лобачевский начал свое исследование с попытки доказать V постулат от противного. За основу рассуждений он берет эквивалентное V постулату утверждение: через точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.

Если предположить, что V постулат неверен, то справедливо утверждение: через точку, не лежащую на данной прямой, проходят, по крайней мере, две прямые, не пересекающие данную прямую.

Проведя цепь логических выводов на основании сделанного предположения и остальных аксиом, Лобачевский хотел прийти к противоречию. Однако по мере того как он развивал все более длинную цепь следствий, у него зрела внутренняя убежденность, что никакого противоречия он не получит. Вместо противоречия он построил весьма своеобразную логически строгую систему геометрических преДЛожений, которую назвал «воображаемой геометрией», и развил до тех же пределов, что и евклидова геометрия. Так была создана геометрия, в которой V постулат не имеет места, — неевклидова геометрия Лобачевского.

Планиметрия Лобачевского строится на основе пяти групп аксиом, из которых первые четыре те же, что и в планиметрии Евклида, а единственная аксиома V группы является отрицанием аксиомы параллельности Евклида. Эту аксиому будем называть аксиомой параллельности Лобачевского и обозначать .

Аксиома . Существуют такая прямая а и такая не лежащая на ней точка А, что через точку А проходит не меньше двух прямых, не пересекающих прямую а.

Множество всех точек будем называть плоскостью Лобачевского.

Приведем некоторые простейшие свойства плоскости Лобачевского, непосредственно вытекающие из аксиом.

Теорема. Сумма углов всякого треугольника меньше . СУМма углов всякого четырехугольника меньше 2. В любом четырехугольнике Саккери Угол при верхнем основании острый.

Теорема. Каковы бы ни были прямая а и не лежащая на ней точка А, через точку А проходит не меньше двух прямых, не пересекающих прямую а.

Теорема. Если у треугольников АВС и А'В'С' равны сООтветствующие углы А и А', В и В', С и С', то эти треугольники равны.

Таким образом, на плоскости Лобачевского нет подобных, но не равных треугольников.

На евклидовой плоскости непересекающиеся прямые называются параллельными. Параллельность прямых на евклидовой плоскости можно характеризовать и другими свойствами, например наличием у них многих общих перпендикуляров или постоянством длин этих перпендикуляров.

На плоскости Лобачевского для двух непересекающихся прямых эти утверждения неверны, И, Возможны два случая: первый — прямые имеют общий перпендикуляр (ясно, что он единственный), второй — прямые не имеют общего перпендикуляра.

Соответственно этим двум случаям на плоскости Лобачевского вводятся понятия расходящихся прямых и параллельных прямых.

Теорема. Каковы бы ни были прямая а и не лежащая на ней точка А, существует бесконечно много прямых, проходящих через точку А и не пересекающих прямую а.

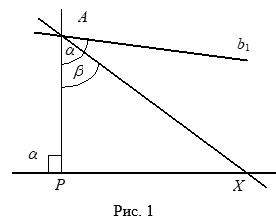
Пусть А — некоторая прямая и А — не лежащая на ней точка. Опустим перпендикуляр АР на прямую А (рис. 1) и проведем через точку А прямую , не пересекающую ПряМую А. Нетупой угол между прямой и перпендикуляром АР обозначим через A. Обозначим , где точная нижняя граница берется по всем прямым, проходящим через точку А и не пересекающим прямую А.

Теорема. СправедлиВО неравенство

.

Угол будем называть Углом параллельности в точке A по отношению к прямой А.

Рассмотрим пучок прямых, проходящих через точку А, не лежащую на данной прямой А, и не пересекающих прямую А. Опустим из точки А перпендикуляр АР на прямую А (рис. 2) и обозначим через И прямые этого пучка, составляющие с лучом АР справа и слева углы, равные . ПРямые и обладают следующим свойством: всякая прямая B, лежащая внутри одной пары вертикальных углов, образованных этими прямыми, не пересекает прямую А, а любая прямая С, лежащая внутри другой пары вертикальных углов, пересекает прямую А; сами прямые и не пересекают А и являются граничными в указанном пучке, отделяющими прямые, пересекающие А, от прямых, не пересекающих А. Прямую будем называть Правой. граничной прямой, прямую — левой.

Граничные прямые пучка прямых, проходящих через точку A и не пересекающих прямую A, называются параллельными прямой A. Одна из них параллельна прямой A вправо, другая – влево.

Две прямые называются РасХодящимися, если они не пересекаются и не параллельны.

Через каждую точку вне данной прямой проходят две прямые, параллельные ей, и бесконечно много прямых, расходящихся с ней; все они лежат внутри пары вертикальных углов, образованных параллельными прямыми.

Теорема. Две прямые, перпендикулярные третьей прямой, расходятся.

Теорема. Две прямые, которые при пересечении с третьей образуют равные накрест лежащие или соответственные углы, расходятся.

Теорема. Всякие две расходящиеся прямые имеют единственный общий перпендикуляр, по обе стороны от которого они неограниченно удаляются одна от другой.

Обратимся теперь к взаимному расположению параллельных прямых на плоскости Лобачевского. Пусть А и B — две прямые и — точка на прямой А. Будем говорить, что прямые А и B Асимптотически сближаются в данном направлении; если длина перпендикуляра, опущенного из точки М прямой A на прямую B, стремится к нулю при неограниченном удалении точки М от точки в данном направлении от точки по прямой A.

Теорема. Две параллельные прямые асимптотически сближаются в сторону параллельности и неограниченно удаляются друг от друга в противоположном направлении.

Результаты исследований Лобачевского и их значения можно кратко сформулировать так: 1 ) V постулат Евклида не является логическим следствием остальных аксиом евклидовой геометрии, ибо существует логически непротиворечивая геометрия (Лобачевского), в которой он не имеет места, в то время как все остальные аксиомы евклидовой геометрии выполняются. 2) Создана новая геометрия, отличная от евклидовой. До работ Н. И. Лобачевского евклидова геометрия представлялась единственно мыслимой теорией пространства. Открытие Лобачевского положило начало далеко идущим обобщениям понятия о пространстве, в цепи этих обобщений неевклидова геометрия Лобачевского явилась первым важнейшим этапом.

Н. И. Лобачевский был первым, но не единственным геометром, открывшим существование неевклидовой геометрии. К выводу о существовании новой геометрии пришел также К. Ф. Гаусс. Однако Он при жизни не опубликовал своих результатов по теории параллельных. После смерти Гаусса в его бумагах были найдены наброски отдельных теорем неевклидовой геометрии. К идее неевклидовой геометрии пришел и венгерский математик Я. Бойаи, который в опубликованной в 1832 г. работе «Аппендикс» изложил ту же теорию, что и Лобачевский, но в значительно менее развитой форме.

Следует отметить, что ученый мир не оцениЛ знаЧЕниЯ Работ Н. И. Лобачевского при его жизни.

Построенная весьма абстрактно (заменой одной аксиомы ее отрицанием), неевклидова геометрия Лобачевского казалась лишенной всякого реального содержания.

< Предыдущая		Следующая >