17. Многочлен. Рациональные дроби. Интегрирование простейших рациональных дробей

Как известно, Многочленом или Целой рациональной функцией называется функция вида

(6)

Где П — Целое положительное число, называемое СтЕПенью многочлена, а — постоянные Числа — Коэффициенты Многочлена.

Корнем многочлена Р(Х) называется всякое число A (действиТельное, мнимое или комплексное), обращающее многочлен в нуль, т. е. такое, что

Напомним ряд теорем, используемых в дальнейшем изложении.

Теорема 1. Всякий многочлЕН имеет по крайнеЙ мере один действительный или комплексный корень.

Далее имеет место теорема Безу:

Теорема 2. Если A корень многочлена Р(Х), то Р(Х) делится На (х - A) без остатка, Т. Е.

(7)

Где Q(X) — многочлен, степень которого на единицу меньше степени многочлена Р(х).

Замечание. Очевидно, коэффициент при старшей степени Х В многочлене Q(X) равен коэффициенту при старШЕй степени Х в многочлене Р(Х).

Теорема 3. Всякий многочлен степени П может быть представлен В виде произведения п линейных множителей вида и постоянного числа A0 — коэффициента при старшей степени х.

Следствие. Многочлен Р(Х) степени п имеет не более Чем п различных корней.

Теорема 4. Если многочлен тождественно равен нулю, то все его коэффициенты равны нулю.

Следствие. Если два многочлена тождественно равны друг другу, то коэффициенты при одинаковых степенях равны между собой.

Пусть Р(Х) — многочлен степени П. По теореме 3 его можно представить в видЕ произведения П линейных множителей

(8)

Среди линейных множИТелей, на которые разложен многочлен, могут быть одинаковые. Объединяя в разложении (8) одинаковые сомножители, мы можем его записать в виде

(9)

Где все числа А, B, ...,L — различны и

Корень А многочлена Р(Х), для которого линейный множитель в разложении (8) встречается Т раз, называется Корнем кратности т. Корень кратности единица называется Простым.

Так, НАпример, многочлен имеет следующие корни: причем 2 есть корень 2-й кратности, -4 — корень кратности 3, а –1 — простой корень. Для многочлена имеет место разложение на множители: , откуда следует, что 1 — корень кратности 2, а –1 — простой корень многочлена Р(Х).

Теперь, когда введено понятие о кратности корня, мы можем уточнить теорему о числе корней многочлена (см. следствие к теореме 3).

Теорема 5. Всякий многочлен П-й степени имеет ровно П Корней, если каждый корень считать столько раз, какова его кратность.

Доказательство этой теоремы непосредственно вытекает из формулы разложения многочлена на линейные множители.

Среди корней многочлена могут быть и Комплексные. Для них имеет место следующая теорема.

Теорема 6. Если многочлен с действительными КоэффиЦиентами имеет комплексный корень , То Сопряженное число также является корнем многочлена.

ТЕОрема 7. Если многочлен с действительными КоэффиЦиентами имеет корнем комплексное число Кратности K, то сопряженное число Также является корнем многочлена той же кратности.

Из этой теоремы непосредственно следует: если в разложении многочлена на множители имеется множитель , соответствующий комплексному корню , то в этом разложении имеется множитель , соответствующий сопряженному корню . Перемножая попарно множители, соответствуюЩие сопряженным корням, получим

Где

Это позволяЕТ заменить произведение линейных множителей, соответствующих Сопряженным корням, квадратным трехчленом с действительными коэффициентами.

Все вышЕИзложенное позволяет высказать следующее окончательное предложение, с помощью которого удается избежать мнимых чисел при разложении многочлена на множители.

Всякий многочлен с действительными коэффициентами можно прЕДставить в следующей форме:

В этом разложении Линейные множители соответствуют действительным корням многочлена, а квадратные трехчлены, соответствуют комплексным корням многочлена.

Постоянные являются действительными числами.

Дробной рациональной функцией или просто рациональной дробью называется функция, равная частному от деления двух многочленов:

Где — многочлен степени Т, a — Многочлен СТепени N.

Например, является рациональной дробью.

Рациональная дробь называется Правильной, если степень числителя меньше степени знаменателя, и Неправильной — В противном случае. Приведенная выше рациональная дробь неправильна.

Многочлен, очевидно, является частным случаем рациональной дроби, знаменатель которой есть многочлен нулевой степени (постоянное число).

Задача настоящей главы заключается в изложении методов интегрирования рациональных дробей, отличных от многочленов. Что касается многочленов, то мы уже знаем, что они легко интегрируются.

Переходя к интегрированию рациональных дробей, отметим, прежде всего, что Всякую неправильную рациональную дробь можно представить в ВИде суммы многочлена и правильной рациональной дроби.

В самом деле, пусть - Неправильная рациональная дробь, т. Е. степень больше или равна степени Q(Х). Разделив числитель на знаменатель, получим тождество

Где и — многочлены, причем степень остатков меньше степени знаменателя дроби .

Например, пусть . Разделив на , получим частное и остаток

Следовательно,

Это замечание показывает, что интегрированиЕ неправильной рациональной дроби сводится к интегрированию многочлена и правильной рациональной дроби :

Так как многочлены мы интегрировать умеем, то задача сводится к интегрированию правильных рациональных дробей.

Как будет показано ниже всякую правильную рациональную дробЬ можно представить в виде суммы конечного числа так называемых Простейших дробей следующих четырех типов:

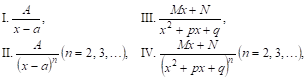
Где А, а, Р, Q, М, N — действительные числа, а трехчлен Не имеет действительных корней, т. е. Поэтому, EcЛи мы научимся интегрировать простейшие ДРоби и разлагать правильную рациональную дробь на сумму простейших, то задача интегрирования рациональных функций будет решена.

Интегрирование простейших дробей I и II типов не представляет никакого труда. В самом деле:

Перейдем теперь к интегрированию рациональных дробей III и IV типов.

Рассмотрим отдельно знаменатель и Дополним до полного квадрата:

Так как по условию трехчлен не имеет действительных корней, то Положим для простоты Применим теперь к интегралу замену переменного, положив тогда

Следовательно,

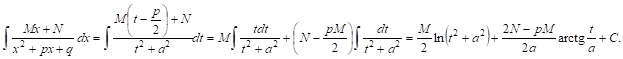
Заменяя, наконец, T И А их выражениями, получим

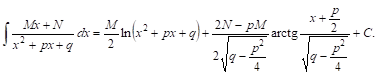
Рассмотрим пример:

Введем новую переменную T, положив ее равной половине производной знаменателя:

Тогда

Следовательно,

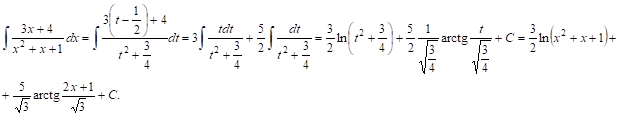
Рассмотрим интегрирование дробей IV типа:

Введем, как и в случае III, новую переменную T, положив Это дает где, как и выше,

Следовательно, (10)

Первый из этих интегралов Соотношения (10) легко вычисляется:

Итак, остается вычислить интеграл Мы здесь предложим способ вычисления этого интеграла с помощью рекуррентной формулы. Мы будем выражать последовательно через , через и т. Д., пока не дойдем до

Итак,

К интегралу применим метод интегрирования по частям, полагая

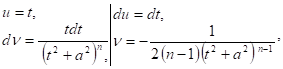
И группируя члены, содержащие , получим

(11)

Это и есть искомая рекуррентная формула. Покажем способ ее применения. Пусть требуется вычислить . Применяя рекуррентную формулу (11), выразим через :

(12)

Применяя ту же рекуррентную формулу для N = 2, выразим через :

Подставляя выражение в (12), найдем

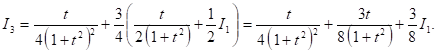
Так как то окончательно

Таким образом, чтобы закончить вопрос об интегрировании рациональных дробей, нам остается Показать, как всякую Правильную раЦиональную дробь можно рАЗложить На сумму Простейших.

Искомая формула разложения правильной рациональной дроби на простейшие состоит в следующем. Пусть знаменатель дроби имеет вид:

Причем квадратные трехчлены в этом выражении не имеют действительных корней, тогда правильную дробь можно представить в виде следующей сумы простейших дробей:

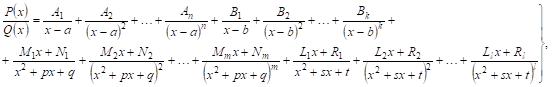(13)

Где - действительные числа. (Примем без доказательства).

Из формулы (13) мы видим, что линейным множителям Знаменателя соответствуют простейшие дроби I и II типа, а квадратным множителям соответствуют простейшие дроби III и IV типа.

При этом число простейших дробей, соответствующих данному множителю (линейному или квадратному), равно степени, с которой этот множитель входит в разложение знаменателя ДроБи на множители.

Для того чтобы можно было пользоваться формулой (13), Надо научиться определять коэффициенты . Этому посвящен следующий подраздел.

< Предыдущая		Следующая >