18. Интегрирование рациональных дробей и некоторых иррациональных функций
Одним из наиболее простых методов определения КоэффициЕнтов в разложении правильной дроби на простейшие является МЕТоД неопределенных коэффициентов. Поясним применение этого метода на примерах.
ПрИМер 1. Разложить на простейшие дроби ![]()
Применим формулу (13):
![]() (14)
(14)
Где ![]() — пока неизвестные постоянные числа.
— пока неизвестные постоянные числа.
Приводим правую часть тождества (14) к общему знаменателю:
![]()
Дроби, стоящие в правой и левой частях последнего равенства, тождественно равны друг другу. Но если две дроби ТождественНо равны друг другу и имеют одинаковые знаменатели, то числители этих дробей также тождественно равны друг другу:
![]()
Раскрывая скобки, располагаем многочлен в правой части последнего равенства по убывающим степеням X:
![]()
Два многочлена тогда и только тогда тождественно равны друг другу, когда коэффициенты при одинаковых стеПЕнях Х равны.
Приравнивая коэффициенты при одинаковых степенях Х в этих многочленах, получим систему уравненИЙ:
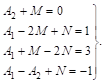
Решив эту систему, найдем:
![]()
Подставив в формулу (14) вместо ![]() найденные значения, получим окончательно
найденные значения, получим окончательно
![]()
Пример 2. Разложить на простейшие дроби:
Так как знаменатель имеет только ДЕйствительные корни, то разложение дроби, согласно формуле (13), имеет вид
![]() (15)
(15)
Приведем правую часть соотношения (15) к общему знаменателю:
![]()
Приравнивая числители, получаем
![]()
Расположим многочлен в правой части по убывающим степеням X:
![]()
Сравнивая коэффициенты при одинаковых степенях Х в правой и левой частях рАВенства, получим систему уравнений:
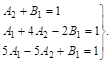
Разрешив эту систему, найдем ![]() Подставив найденные значения коэффициентов в соотношения (15), получим
Подставив найденные значения коэффициентов в соотношения (15), получим
![]()
Пример 3. Разложить на простейшие дроби ![]()
Знаменатель имеет только комплексные корни; в этом случае разложение дроби на простейшие примет вид
![]()
Приведя к общему ЗНаменателю выражение, стоящее в правой части, придем к тождеству:
![]()
Откуда:
![]()
Приравнивая коэффициенты при одинаковых степенях, приходим к системе уравнеНИй:
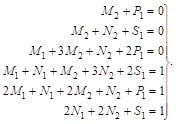
Решая эту систему уравнений, найдем
![]()
Таким образом,
![]()
Пример 4. Разложить на простейшие дроби ![]()
Применяя формулу (13), получим:
![]()
Приводя к общему знаменателю, получим тождество
![]()
Или
![]()
Приравнивая коэффициеНТы при одинаковых сТЕпенях X , получим систему уравнений:
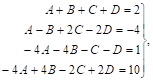
Из которой находим
![]()
Следовательно,
![]()
Часто нахождение коэффициентов разложения значительно упрощается, если применить так называемый Метод Произвольных значений. Рассмотрим с этой точки зрения только что приведенный пример. Полученное там равенство
![]() (16)
(16)
Есть тождество, справедливое при любом значении Х.
Выбираем такие значения Х, для которых равенство (16) принимает наиболее простой вид. Здесь проще всего за Х взять один из корней знаменателя.
![]()
Откуда ![]()
Аналогично, полагая Х = -1, найдем 3 = 6В, B =![]() ; пpи X = 2, 12 = 12С, С = 1; при Х = -2, -24 = -12D; D = 2.
; пpи X = 2, 12 = 12С, С = 1; при Х = -2, -24 = -12D; D = 2.
На практике указанныЙ метод целесообразно применять в случае, когда знаменатель Q(Х) правильной рациональной дроби ![]() имеет только действительные простые корни.
имеет только действительные простые корни.
Все выше изложенное позволяет нам сформулировать основные правила интегрирования рациональных дробей.
1. Если рациональная дробь неправильная, то ее представляют в виде суммы многочлена и правильной рациональной ДРоби.
Тем самым интегрирование неправильной рациональной дроби сводится к интегрированию многочлена и правильной рациональной дроби.
2. Разлагают знаменатель правильной дроби на множители.
3. Правильную рациональную дробь представляют в виде суммы простейших дробей и сводят интегрирование правильной рациональной дроби к интегрированию простейших дробей.
Рассмотрим примеры:
Пример 1. ![]()
Под интегралом стоит неправильная рациональная дробь. Выделяя целую часть, получим
![]()
Следовательно,
![]()
Разложим правильную рациональную дробь ![]() на простейшие дроби:
на простейшие дроби:
![]()
Поэтому
![]()
Таким образом, окончательно имеем:
![]()
Пример 2. ![]()
ПоД интегралом стоит правильная рациональная дробь.
Разлагая ее на простейшие дроби, получим ![]()
Следовательно, ![]()
Что касается интеграла в правой части, то он берется, как мы знаем, подстановкой ![]() При этом
При этом ![]()
![]()
![]() Таким образом, имеем:
Таким образом, имеем:
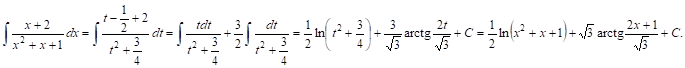 Итак,
Итак, ![]()
![]()
Интеграл от рациональной дроби является элементарной функцией. Мы сейчас рассмотрим некоторые типы интегралов, которые надлежащей заменой переменного могут быть сведены к интегралам от рациональных функций, следовательно, также могут быть выражены через элементарные функции.
Предварительно рассмотрим некоторые новые понятия. Многочленом относительно перемЕНных и и V Называется сумма произведений вида: ![]() , где Т и П — целые неотрицательные числа.
, где Т и П — целые неотрицательные числа.
Например, выражения ![]()
![]()
![]() U являются многочленами относительно И и V.
U являются многочленами относительно И и V.
Частное от деления двух многочленов относительно И и V называется Рациональной функцией от и и V или Рациональным выражением относительно И и V.
Например, дроби ![]() являются рациональными выражениями относительно И и V. Рациональную функцию от И и V обозначают
являются рациональными выражениями относительно И и V. Рациональную функцию от И и V обозначают ![]() .
.
Легко заметить, что сумма, разность, произведение и частное нескольких рациональных функций от И и V есть тоже рациональная функция от U и V.
Рациональным выражением относительно функций ![]() и
и ![]() называется рациональная функция от И и V, в которую вместо И И V подставлены соответственно
называется рациональная функция от И и V, в которую вместо И И V подставлены соответственно ![]() и
и ![]() . Рациональное выражение относительно
. Рациональное выражение относительно ![]() и
и ![]() обозначают
обозначают ![]() . Аналогичный смысл имеет выражение
. Аналогичный смысл имеет выражение ![]() .
.
Пример 1. ![]() - рациональное выражение ОтносиТельно X И
- рациональное выражение ОтносиТельно X И ![]()
Пример 2. ![]() - рациональное выражение относительно
- рациональное выражение относительно ![]() и
и ![]()
Заметим, что Если ![]() и
и ![]() — Рациональные функции от х, то
— Рациональные функции от х, то ![]() Также является рациональной функцией от х.
Также является рациональной функцией от х.
1. Интегралы вида ![]() , Где п — Целое число, могут быть сведены к интегралам от рациональных функций. Докажем это.
, Где п — Целое число, могут быть сведены к интегралам от рациональных функций. Докажем это.
Произведем в этом интеграле замену переменной, положив ![]() тогда
тогда ![]() Следовательно,
Следовательно, 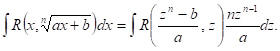
Интеграл, стоящий в правой части равенства, есть интегРАл от рациональной функции относительно переменной интегрирования Z и, следовательно, может быть вычислен в элементарных функциях.
Поясним сказанное примерами:
Полагаем ![]() ; тогда
; тогда ![]() и
и ![]()
Следовательно, ![]()
Таким образом, мы свели наш интеграл к интегралу от рациональной функции.
![]()
Подставляя вместо Z его выражение через Х, т. Е. ![]() Имеем:
Имеем:
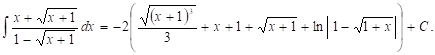
Пример 2. ![]() Подынтегральное ВыражеНие рационально зависит от
Подынтегральное ВыражеНие рационально зависит от ![]() , так как
, так как ![]() Сделаем замену переменной:
Сделаем замену переменной: ![]() , откуда
, откуда ![]() и
и ![]()
Следовательно,
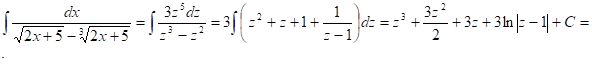
![]() .
.
II. ИнтЕгРалы болЕЕ общего вида: 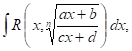 где R — рациОНальное ВЫражЕНие, от х U
где R — рациОНальное ВЫражЕНие, от х U ![]() такжЕ приводятся к интегралам от рациональной функции, если полоЖИТЬ
такжЕ приводятся к интегралам от рациональной функции, если полоЖИТЬ ![]()
Пример. Вычислить 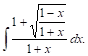
Полагаем ![]() откУДа
откУДа ![]()
![]()
Следовательно,
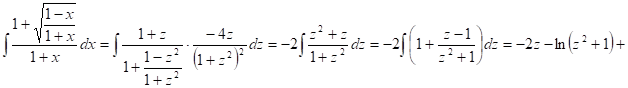
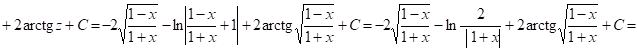
![]()
| < Предыдущая | Следующая > |
|---|