16. Метод замены переменной, интегрирование по частям
Во многих случаях удается введением вместо X новой переМенной Z, связанной с Х некоторым соотношением, свести интеграЛ ![]() к новому интегралу, который содержится в таблице ИЛи легко находится другим методом. Этот метод интегрирования получил название Метода замены переменной или метода интегрироВАния ПодстаноВКой.
к новому интегралу, который содержится в таблице ИЛи легко находится другим методом. Этот метод интегрирования получил название Метода замены переменной или метода интегрироВАния ПодстаноВКой.
Введем вместо Х новую переменную Z, связанную с Х соотНОшенИЕм ![]() , где
, где ![]() — непрерывная, строго монотонная функция, имеющая непрерывную производную
— непрерывная, строго монотонная функция, имеющая непрерывную производную ![]() . Покажем, что тогда имеет место равенство
. Покажем, что тогда имеет место равенство
![]() (1)
(1)
Формула (1) называется формулой замены переменного. Для доказательства соотношения (1) достаточно убедиться, что дифференциалы обеих его частей равны.
Дифференцируя левую часть соотношения (1), имеем:
![]()
Но так как ![]() то
то ![]() Это дает
Это дает
![]() (2)
(2)
С другой стороны, дифференцируя правую часть соотношения (1), имеем:
![]() (3)
(3)
Соотношения (2) и (3) показывают, что
![]()
Откуда следует равенство интегралов:
![]()
Таким образом, формула (1) доказана.
Допустим, что функция ![]() такова, что интеграл, стоящий в правой части соотношения (1), легко находится. Пусть
такова, что интеграл, стоящий в правой части соотношения (1), легко находится. Пусть
![]()
Тогда для нахождения интеграла ![]() достаточно разрешить уравнение
достаточно разрешить уравнение ![]() относительнО Z, т. Е. найти обратную функцию
относительнО Z, т. Е. найти обратную функцию ![]() и подставить ее в Ф(Z):
и подставить ее в Ф(Z):
![]()
Замечание. Формулу (1) легко запомнить. Ее правая часть получается, если в интеграле ![]() формально заменИТь Х На
формально заменИТь Х На ![]() , a Dx на
, a Dx на ![]() .
.
Рассмотрим несколько примеров.
Пример 1. ![]()
Положив ![]() , находим Dx = Adz. ПримЕНяя, формулу (1), получаем
, находим Dx = Adz. ПримЕНяя, формулу (1), получаем
![]()
Но интеграл ![]() согласно формуле VIII.
согласно формуле VIII.
Поэтому ![]()
Возвращаясь снова к переменной Х, получим
![]()
Пример 2. ![]()
Полагая ![]() ,
, ![]() и применяя формулу (1), имеем:
и применяя формулу (1), имеем:
![]()
Если под интегралом стоит суперпозиция двух функций, умноженная на производную от внутренней функции, то вычисления обычно упрощаются, если заменить внутреннюю функцию новой переменной. Действительно, применяя тогда формулу замены переменной, получим
![]()
Где ![]() . Заметим, что эта формула отличается от формулы (1) только обозначением независимых переменных.
. Заметим, что эта формула отличается от формулы (1) только обозначением независимых переменных.
Пример 3. ![]()
ЭТО дает: Dz = CosXdx и
![]()
УдачноЙ заменой переменного мы свели наш интеграл к интегралу от степенной функции.
Так как
![]()
То
![]()
Пример 4. ![]()
![]()
Замечая, что ![]() положим
положим ![]() Это дает
Это дает ![]() и, следовательно,
и, следовательно,
![]()
Таким образом,
![]() (XI)
(XI)
Пример 5. ![]()
Полагая ![]() имеем:
имеем: ![]()
![]()
Итак,
![]() (XII)
(XII)
Пример 6. ![]()
Этот интеграл, конечно, можно было бы вычислить методом разложения, если ![]() разложить по формуле бинома Ньютона. Но это привело бы к слишком громоздким вычислениям. Однако, замечая, что
разложить по формуле бинома Ньютона. Но это привело бы к слишком громоздким вычислениям. Однако, замечая, что ![]() , мы видим, что заменой переменной
, мы видим, что заменой переменной ![]() наш интеграл сводится к интегралу от степенной функции. В самом деле, пусть
наш интеграл сводится к интегралу от степенной функции. В самом деле, пусть ![]() ; тогда
; тогда ![]() . Это дает
. Это дает
![]()
Возвращаясь к переменной Х, окончательно получим
![]()
Пример 7. ![]()
Заметим, что диффЕРенциал знаменателя отличается от числителя на постоянный множитель — 5; поэтому напрашивается следующая замена переменной: ![]() , откуда
, откуда ![]() и, СлеДовательно,
и, СлеДовательно,
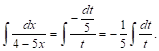
Из таблицы находим: ![]() Поэтому
Поэтому
![]()
Пример 8. Интегралы в примерах 4, 5, 7 являются частными СЛучаями интеграла более общего вида:
![]()
Т. Е. интеграла от дроби, числитель которой является дифференциалом знаменателя.
Полагая ![]() , имеем
, имеем ![]() ,
,
![]()
Так, например, ![]()
Так как
![]()
С приобретением навыка в интегрировании, можно не производить в простейших интегралах подробно всех выкладок, связанных с заменой переменной. Покажем это на примерАХ.
Замечая, что ![]() и вводя поправку
и вводя поправку ![]() , имеем:
, имеем:
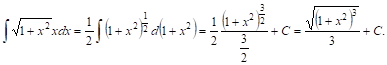
Замечая, что ![]() , имеем согласНО формуле X:
, имеем согласНО формуле X:
![]()
Пример 11. ![]()
![]()
Часто применяют одновременно метод интегрирования разложением и метод замены переменной.
Пример 12. ![]()
Так как ![]() а
а ![]()
То ![]()
Метод интегрирования по частям состоит в следующем. Пусть ![]() и
и ![]() — Две функции от Х, имеющие непрерывные производные. Известно, что
— Две функции от Х, имеющие непрерывные производные. Известно, что
![]() (4)
(4)
Интегрируя обе части равенства (4), имеем:
Откуда
![]() (5)
(5)
Произвольной постоянной, получившейся при интегрировании выражения D(Uv), мы не пишем, включая ее мысленно в оставшийся в правой части интеграл ![]() .
.
Формула (5) называется Формулой интЕГрирования по частям, Она дает возможность свести вычисление интеграла ![]() к вычислению интеграла
к вычислению интеграла ![]() .
.
Для успешного применения этого метода целесообразно пользоваться следующими общими указаниями:
1. Подынтегральное выражение разбивают на 2 множителя: И и DN (множиТЕль DN обязательно содержит Dx).
2. Множитель Dv выбирается так, чтобы по нему можно было бы найти первообразную V.
3. Интеграл ![]() должен получиться, вообще говоря, проще, чем данный интеграл.
должен получиться, вообще говоря, проще, чем данный интеграл.
ПояСНим применение этого метода примерами.
Имеется несколько возможностей. Например, Можно положить ![]() , a
, a ![]() , можно положить
, можно положить ![]() , a
, a ![]()
Полагая ![]() найдем
найдем 
Применяя формулу (5), получаем
![]()
Это разбиение на множители следует признать неудачНЫм, так как оно приводит к более сложному интегралу.
Положим теперь
![]() отсюда найдем
отсюда найдем ![]()
Применяя формулу (5), имеем:
![]()
Но ![]() Поэтому окончательно получаем
Поэтому окончательно получаем
![]()
Следовательно, это разбиение Подынтегрального выражения на множители следует признать удачным.
Положим
![]() ; это дает
; это дает 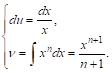
Применяя формулу (5), получим
![]()
Таким образом,
![]()
Иногда для получения окончательного результата ЦелесообРазно интегрирование по частям применять послеДОвательно несколько раз.
Укажем на некоторые, часто встречающиеся интегралы, которые вычисляются методом интегрирования по частям.
I. Интегралы вида: ![]() ГДе Р(Х) — Многочлен, а — Постоянное число, легко берутся методом интегрирования по частям, если положить Р(Х)=И.
ГДе Р(Х) — Многочлен, а — Постоянное число, легко берутся методом интегрирования по частям, если положить Р(Х)=И.
Применяя этот метод, например, к интегралу ![]() Получим
Получим
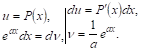
Следовательно, ![]()
Второй интеграл является интегралом того ЖЕ типа, что и первый, но степень многочлена Р'(Х) на единицу ниже степени многочлена Р(Х). Применяя к нему снова интегрирование по частям и повторяя его столько раз, какова степень многочлена сведем, в коНЦе концов, наш ИНтеграл к интегралу ![]() .
.
Таким же путем вычисляются и интегралы ![]()
Положим
![]()
Применяя формулу интегрирования по частям, получим
![]()
К последнему интегралу снова применяем метод интегрирования по частям:

![]()
Следовательно,
![]()
Изложенный метод интегрирования показывает, что интегралы вида ![]() Где Р(Х) — многочлен, всегда берутся в элементарных функциях. В отличие от них, интегралы
Где Р(Х) — многочлен, всегда берутся в элементарных функциях. В отличие от них, интегралы ![]() где R(X) — Рациональная дробь, не всегда интегрируются в элементарных функциях. Так, например, интегралы
где R(X) — Рациональная дробь, не всегда интегрируются в элементарных функциях. Так, например, интегралы ![]() Не выражаются в элЕмЕнтарных функциях.
Не выражаются в элЕмЕнтарных функциях.
II. Интегралы ВИда: ![]() Где Р(Х) — Многочлен, всегда берутся методом интегрирования по частям, если за И принять трансцендентную функцию, являющуюся множителем при Р(Х). Рассмотрим примеры.
Где Р(Х) — Многочлен, всегда берутся методом интегрирования по частям, если за И принять трансцендентную функцию, являющуюся множителем при Р(Х). Рассмотрим примеры.
Пример 1. ![]()
Полагаем 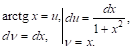
Формула (5) дает: ![]()
Пример 2. ![]()
Полагаем 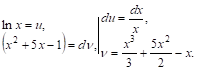
Следовательно,
![]()
III. Вычисление интегралов вида: ![]()
Укажем, наконец, еще на один случай, когда интегрироВАние по частям приводит к цели. Пусть нам надо вычислить иНТеграл ![]()
Допустим, что после однократного или двукратного интегрирования по частям оказалось возможным представить этот интеграл в виде суМмЫ некоторой известной функции и интеграла от F(X), причем перед интеграЛОм стоит коэффициент K, отличный от единицы:
![]()
Тогда, перенося второе слагаемое в левую часть, получим
![]()
Откуда ![]() где
где ![]() одна из первообразных от ВыражеНия
одна из первообразных от ВыражеНия ![]() . Чтобы НАйти семейство всех первообразных (т. Е. неопределенный интеграл) остается к правой части добавить произвольное постоянное С:
. Чтобы НАйти семейство всех первообразных (т. Е. неопределенный интеграл) остается к правой части добавить произвольное постоянное С:
![]()
Интегралы вида ![]() берутся с помощью только что указанного приема. Рассмотрим конкретный пример:
берутся с помощью только что указанного приема. Рассмотрим конкретный пример:
Пример. ![]()
Положим 
Тогда ![]()
К последнему интегралу снова применим интегрирование по частям, положив

Тогда
![]()
Следовательно:
![]()
Определяем отсюда ![]()
![]()
Мы разобрали основные методы интегрирования. Перейдем тЕПерь к систематическому изучению того, как применяются эти методы к интегрированию конкретных классов элементарных функций. Для дальнейшего изложения нам понадобятся некоторые сведения о многочленах, которые мы приводим в слеДующем Пункте.
| < Предыдущая | Следующая > |
|---|