15. Введение первообразной и неопределенного интеграла

В дифференциальном исчислении мы решали следующую основную задачу: по данной функции найти ее производную. Многочисленные вопросы науки и техники приводят к постановке обратной задачи: для функции , определенной на сегменте (или интервале), найти такую функцию , производная которой равнялась бы заданной функции , т. е.

(1)

Назовем произведение F (X)Dx — дифференциальным выражением. Тогда только что поставленную задачу можно сформулировать в следующей, равносильной ей форме: для данного дифференциального выражения F(X)Dx найти такую функцию , дифференциал которой равнялся бы заданному дифференциальному выражению, т. е.

(2)

Функция F(X), связанная с функцией F(x) соотношением (1) или (2), называется ее Первообразной.

Таким образом,

Первообразной от данной функции f(x) называется функция, производная которой равна данной функции, или, что то же самое, дифференциал которой равен дифференциальному выражению f (х) dx.

Так, например, первообразной от функции будет функция , так как , или, что то же самое, .

Отыскание по данной функции ее первообразной составляет одну из основных задач интегрального исчисления. Действие — отыскание первообразной — называется интегрированием функции. При этом, естественно, возникает следующий вопрос: для всякой ли функции существует первообразная?

Утвердительный ответ на этот вопрос для достаточно широкого класса функций дает следующая теорема, принимаемая нами без доказательства.

Теорема 1. Любая непрерывная на сегменте функция имеет на этом сегменте первообразную.

На протяжении всего нашего изложения функции, для которых ищутся первообразные, мы будем считать непрерывными.

Если же функция, для которой мы ищем первообразную, имеет точки разрыва, то мы будем ее рассматривать только в интервалах непрерывности.

Задача отыскания по данной функции ее первообразной решается неоднозначно. В самом деле, если, например, , то первообразной для нее является не только функция (-cos Х), но также и , и , и вообще , где С — Произвольное число. Как мы сейчас докажем, функция Не имеет других первообразных, кроме тех, которые могут быть представлены в виде: - . Это будет вытекать из следующей общей теоремы.

Теорема 2. Если функция есть первообразная для функции на сегменте [А; B], то всякая другая первообразная для отличается от на постоянное слагаемое, т. е. может быть представлена в виде: где С — постоянное число.

ПреДВарительно сформулируем без доказательства лемму, из которой непосредственно следует теорема 2.

Лемма. Функция, производная которой во всех точках сегмента [а; B] равна нулю, постоянна на этом сегменте.

Перейдем теперь к доказательству теоремы 2.

Доказательство теоремы 2. Пусть — какая-либо первообразная функция от , а Ф(Х) — Любая другая первообразная от той же функции; таким образом, на [А; B]. Производная разности равна нулю всюду на сегменте [А; B], так как

Но функция, производная которой всюду на сегменте [А; B] равна нулю, в силу леммы, постоянна на этом сегменте, т. е. , где С — постоянное число. Таким образом,

Теорема 2 показывает, что выражение где — Некоторая первообразная для функции , а С — произвольная постоянная, охватывает совокупность всех первообразных от данной функции .

Введем теперь основное понятие — понятие Неопределенного интеграла.

Если — одна из первообразных для функции , то выражение где С — произвольная постоянная, называется неопределенным интегралом от этой функции.

Неопределенный интеграл от функции обозначается символом (читается: «неопределенный интеграл на Dx»).

Следовательно,

При этом называется Подынтегральной функцией, — Подынтегральным выражением, х — Переменной интегрирования, А символ ∫ — Знаком неопределенного интеграла.

Под знаком интеграла мы пишем не производную искомой функции, а ее дифференциал.

Полагая, например, , имеем

Из самого определения первообразной следует, что дифференциал этой первообразной равен подынтегральному выражению. Так как это утверждение имеет место для любой первообразной от данной функции, его кратко можно выразить следующим образом:

1. Дифференциал от неопределенного интеграла равен подынтегральному выражению, Т. е.

(3)

Отметим, наконец, еще одно свойство, которое, как и свойство 1, устанавливает связь между операциями дифференцирования и интегрирования.

2. Неопределенный интеграл от дифференциала некоторой функции равен самой ЭТой функции плюс произвольная постоянная.

В самом деле, пусть — Дифференцируемая функция, для которой

Следовательно,

Но . Поэтому

Например:

Свойства 1 и 2 означают, что дифференцирование и интегрирование являются взаимно обратными действиями.

Рассмотрим некоторые задачи, приводящие к неопределенному интегралу.

Задача 1. Требуется найти кривую, у которой тангенс угла наклона касательной в каждой ее точке есть заданная функция абсциссы этой точки.

Пусть — уравнение искомой кривой. Согласно геометрическому смыслу производной, тангенс угла наклона касательной к кривой В точке с абсциссой Х равен значению производной в этой точке. Значит, нам нужно найти такую функцию , для которой

. (4)

Соотношение (4) показывает, что искомая функция Является первообразной для . Следовательно, наша задача свелась к основной задаче интегрального исчисления — к нахождению первообразной от данной функции. Поэтому уравнение искомой кривой имеет вид

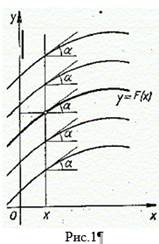
Мы видим, что условию задачи удовлетворяет не одна кривая, а семейство кривых. Если есть одна из таких кривых, то всякая другая может быть получена из нее параллельным переносом вдоль оси Оу (рис. 1).

Назовем график первообразной функции от — Интегральной кривой.

Неопределенный интеграл геометрически представляет совокупность всех интегральных кривых.

Все кривые из этой совокупности могут быть получены из одной интегральной кривой параллельным сдвигом в

Направлении оси Оу.

Для того чтобы из данного семейства кривых выделить одну определенную кривую, нужно к условию задачи присоединить дополнительное условие, например, потребовать, чтобы кривая проходила через данную точку . Такое условие называется Начальным. Задание начального условия, вообще говоря, позволяет выделить из семейства всех интегральных кривых вполне определенную кривую, а именно ту кривую, которая проходит через точку . Координаты этой точки должны удовлетворять уравнению искомой кривой , т. е. . Из этого условия однозначно определяем С: . Следовательно, уравнение искомой интегральной кривой имеет вид:

Рассмотрим конкретный пример.

Через точку (1; 2) провести кривую, у которой угловой коэффициент касательной в каждой точке с абсциссой Х равен 3Х2.

Имеем У'=3Х2. Легко сообразить, что одной из первообразных для 3Х2 будет Х3. Следовательно,

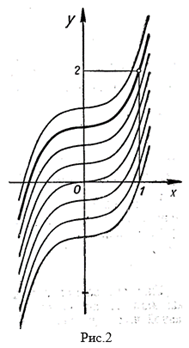
Итак, кривые, для которых в точках с абсциссой Х тангенс угла наклона касательной равен 3Х2, образуют семейство кубических парабол (рис.2). Из этого семейства кривых нам нужно выбрать ту кривую, которая проходит через точку (1; 2) (начальное условие). Поэтому откуда С = 1. Таким образом, уравнение искомой кривой будет:

Задача 2. Теперь рассмотрим задачу из совершенно другой области.

Материальная точка массы Т движется по вертикальной прямой под действием силы тяжести. Определить путь, Пройденный Точкой за время T, если в начальный момент Точка имела скорость . Примем за ось Ох вертикальную прямую, по которой движется точка; при этом за положительное направление оси примем направление к земле, а за начало координат примем точку, соответствующую положению материальной точки в начальный момент (при T=0, Х=0). Пройденный точкой путь Х будет некоторой функцией времени: . Наша задача заключается в том, чтобы определить вид этой функции, т.Е. зависимость пройденного пути от времени T.

Из физики известно, что скорость падающего тела за каждую секунду возрастает на величину G). Поэтому, если при T=0 скорость материальной точки равна нулю, то к моменту времени T скорость точки V возрастает до значения Gt. Таким образом,

(5)

С другой стороны, мы знаем, что скорость есть производная пути по времени: . Следовательно, приравняв два найденных выражения для скОРости, найдем

(6)

Соотношение (6) показывает, что искомая функция Является первообразной для функции Gt. Поэтому

).

Постоянную С находим из начального условия: при , . Следовательно, т. е. С=0.

Таким образом, путь Х, пройденный точкой к моменту времени T, выразится следующей формулой, хорошо известной из курса физики

Уже эти элементарные примеры показывают, что поставленная нами задача об отыскании для данной функции ее первообраЗНой имеет не только формально математический интерес, как операция, обратная дифференцированию, но что к этой задаче мы непосредственно приходим при решении целого ряда вопросов естествознания и техники.

< Предыдущая		Следующая >