10. Использование понятия производной при нахождении пределов

Мы уже знакомы с приемами нахождения пределов отношения двух бесконечно малых или бесконечно больших функций, то есть раскрытие неопределенностей вида И .

Рассмотрим новое правило для раскрытия этих неопределенностей – правило Лопиталя.

Правило Лопиталя. Предел отношения двух бесконечно малых или бесконечно больших функций (неопределенность 0/0 или ¥/¥) равен пределу отношения их производных:

если предел, записанный в правой части этого равенства, существует.

Поясним на примерах.

Пример 1. Найти .(Аналогичный пример мы решали, не используя понятия производной, воспользуемся теперь правилом Лопиталя)

Решение. Имеем

Если отношение производных опять представляет собой неопределенность вида 0/0 или ¥/¥, то можно снова применить правило Лопиталя, т. е. перейти к отношению вторых производных и т. д.

Пример 2. Найти .

Решение. Здесь также числитель и знаменатель одновременно стремятся к нулю. Применяя два раза правило Лопиталя, находим

Пример 3. Найти .

Решение. Здесь числитель и знаменатель представляют собой бесконечно большие функции при x®+¥. Применяя два раза правило Лопиталя, находим

Кроме рассмотренных случаев неопределенностей вида 0/0 и ¥/¥, встречаются еще неопределенности следующих видов.

Неопределенность вида ¥ - ¥. Под раскрытием такой неопределенности понимают нахождение предела, когда являются бесконечно большими функциями одного знака, т. е. .

Этот случай преобразованием выражения сводится к неопределенности вида 0/0 или ¥/¥.

Пример 4. Найти .

Решение. Если ; следовательно, имеем неопределенность вида ¥ -¥. Выполним следующие преобразования:

При числитель и знаменатель в последнем выражении одновременно стремятся к нулю. Таким образом, получаем неопределенность вида 0/0. Применяя правило Лопиталя, найдем

Итак, .

Неопределенность вида . Под раскрытием такой неопределенности понимают нахождение предела , если . Этот случай также преобразованием выражения сводится к раскрытию неопределенностей вида 0/0 или ¥/¥.

Пример 5. Найти

Решение. Так как , то имеем неопределенность вида . Преобразуем данное выражение так:

Поскольку здесь мы получили уже неопределенность вида 0/0, можно применить правило Лопиталя:

Неопределенность вида 1¥. Под раскрытием такой неопределенности понимают нахождение предела , если .

Неопределенность вида 00. Под раскрытием такой неопределенности понимают нахождение предела, если .

Неопределенность вида ¥0. Под раскрытием такой неопределенности понимают нахождение предела , если .

Неопределенность вида 1¥, 00 и ¥0 приводятся к случаям неопределенностей вида 0/0 или ¥/¥ обычно с помощью логарифмирования .

Пример 6. Найти .

Решение. В этом случае , и мы имеем неопределенность вида ¥0. Обозначим Логарифмируя, находим

Так как при x®+¥ числитель и знаменатель стремятся к бесконечности, то получаем неопределенность вида ¥/¥. Применяем правило Лопиталя:

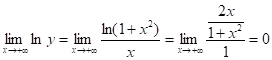
Так как ln y – функция непрерывная, то ; следовательно, . Итак, .

Замечание. Согласно правилу Лопиталя, если существует предел отношения производных данных функций, то существует и предел отношения самих функций. Если же предел отношения производных не существует, то это еще не означает, что не существует предел отношения самих функций. Рассмотрим, например, две бесконечно большие функции при x®+¥: . Предел их отношения при x®+¥ существует, так как

Однако предел отношения производных данных функций

Не существует, так как cos x при x®+¥ не имеет предела.

Вопросы для самопроверки:

1. Что называется производной?

2. Что назвается производными высших порядков?

3. Может ли функция быть непрерывной, но не дифференцируемой?

4. Может ли функция быть дифференцируемой, но не непрерывной?

5. Что называется дифференциалом?

6. Сформулируйте правило Лопиталя?

< Предыдущая		Следующая >