08. Связь непрерывности и дифференцируемости функции

Из уже известных нам свойств пределов очевидно, что если функция у(x) имеет конечный предел ,

То предел произведения этого соотношения на бесконечно малую тем более конечен и, более того, равен нулю.

, а – это означает непрерывность функции. То есть если функция дифференцируема, то она непрерывна.

То, что обратное неверно, видно из примера:

1. Рассмотрим функцию в точке

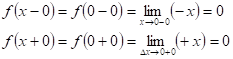
Предел слева существует, конечен и равен пределу справа, и значение функции в точке совпадает со значением предела.

Следовательно, функция непрерывна в нуле.

2. Выражение для производной функции у

, то есть отношение имеет в точке x=0 левый предел (-1), а правый предел – (+1), а это означает, что предела она не имеет, то есть производной в точке х=0 не существует.

Видим, что функция, непрерывная в точке х=0, производной в этой точке не имеет.

< Предыдущая		Следующая >