04. Основные элементарные функции. Пределы элементарных функций. Свойства пределов
К основным элементарным функциям относятся:
1) степенная функция y=xn
2) показательная функция y=ax
3) логарифмическая функция y=logax
4) тригонометрические функции y=sin x, y=cos x, y=tg x, y=ctg x
5) обратные тригонометрические функции y=arcsin x, y=arccos x, y=arctg x, y=arcctg x.
Предел элементарной функции в точке ее определения равен частному значению функции в этой точке ![]()
Это свойство функций и называется непрерывностью в точке х0.
Функции, полученные из основных элементарных с помощью конечного числа арифметических действий и конечного числа композиций, называются элементарными.
При вычислении пределов функций обычно пользуются следующими основными теоремами о пределах:
1. ![]() , где С-константа 2.
, где С-константа 2. ![]() Константа выносится изпод знака предела.
Константа выносится изпод знака предела.
Если пределы ![]() существуют и конечны, то
существуют и конечны, то
3. ![]() Предел суммы (разности) равен сумме (разности) пределов.
Предел суммы (разности) равен сумме (разности) пределов.
4. ![]()
5. 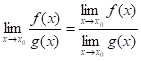 , если
, если ![]()
Предел произведения равен произведению пределов. Предел частного равен частному пределов.
Нарушение ограничений, накладываемых на функции при вычислении их пределов, приводит к неопределенностям.
Например, зная лишь, что ![]() Нельзя сказать заранее, чему равен
Нельзя сказать заранее, чему равен ![]()
Говорят, что имеет место Неопределенность вида ![]()
Элементарными приемами раскрытия неопределенностей являются:
1) сокращение на множитель, создающий неопределенность
2) деление числителя и знаменателя на старшую степень аргумента (для отношения многочленов при x®¥)
3) применение эквивалентных бесконечно малых и бесконечно больших
4) использование двух замечательных пределов:
Первый замечательный предел ![]()
Второй замечательный предел![]() ,
,
А также следующие свойства (*)
![]() если
если ![]() , т. е.
, т. е. ![]() .
.
![]() если
если ![]() , т. е.
, т. е. ![]() .
.
![]() если
если ![]() а
а ![]() , т. е.
, т. е. ![]() .
.
![]() если
если ![]() А
А ![]() , т. е.
, т. е. ![]() .
.
Рассмотрим конкретные примеры пределов:
1. Найдем
![]()
Воспользуемся свойством предела суммы:
![]()
Воспользуемся свойствами о пределе константы и выносе константы за знак предела:
![]()
Так как под знаком предела у нас находятся основные элементарные функции, подставляем вместо х его предельное значение 1 и получаем: Z1=3+2+5=10
2.Найдем
![]()
Под знаком предела стоит композиция основных элементарных функций – элементарная функция. Подставляем вместо х его предельное значение равное 3, получаем в числителе бесконечно большую, а в знаменателе бесконечно малую функцию.
![]()
3. Найдем
![]()
Так как ![]() Существует и конечен,
Существует и конечен, ![]() Существует, конечен и не равен 0, то
Существует, конечен и не равен 0, то

4. Найдем
![]()
Подстановка предельного значения в знаменатель дает предел, равный нулю. Следовательно мы имеем отношение константы к бесконечно малой (соотношения *) { c/0}
![]()
5. Найдем
![]()
Подстановка предельного значения приводит к неопределенности. ![]() Затем делим на старшую степень х~х2.
Затем делим на старшую степень х~х2.
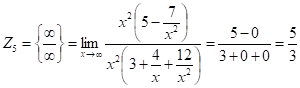
6. Найдем
![]()
Подстановка предельного значения аргумента приводит к неопределенности типа ![]() . Так как под знаком предела стоит отношение двух многочленов, то разделим числитель и знаменатель на старшую степень аргумента, т. е. на х4.
. Так как под знаком предела стоит отношение двух многочленов, то разделим числитель и знаменатель на старшую степень аргумента, т. е. на х4.
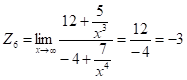 поскольку при x®¥ функции
поскольку при x®¥ функции ![]() являются бесконечно малыми.
являются бесконечно малыми.
7. Рассмотрим неопределенность вида {¥ -¥}
![]()
При раскрытии неопределенности этого вида достаточно домножить и разделить выражение под знаком предела на сопряженное ему выражение
![]()
8. Неопределенность вида {0/0}.
![]()
При подстановке предельного значения получается неопределенность вида {0/0}. Это вызвано тем, что и многочлен в числителе и многочлен в знаменателе имеют –1 своим корнем. Следовательно, надо сократить дробь на критический множитель х+1 выделив его предварительно:
![]()
![]()
Подставляем предельное значение и пользуясь свойствами пределов, получаем:
![]()
9. Найдем
![]()
Имеем неопределенность вида {0/0} в тригонометрическом выражении. Раскроем ее с помощью первого замечательного предела, но в первом замечательном пределе знаменатель дроби и аргумент синуса должны совпадать. Следовательно, домножим и разделим на 5х, чтобы получить ![]()
![]() так как при
так как при ![]() То первый сомножитель стремится к единице и
То первый сомножитель стремится к единице и
![]()
10. Найдем ![]()
Z10 содержит неопределенность {0/0} в тригонометрическом выражении. Попытаемся обратиться к первому замечательному пределу. Для этого надо числитель заменить выражением, содержащим синус по известной тригонометрической формуле cos двойного угла:
![]()
11. Найдем
![]()
Здесь неопределенность {0/0}, к которой приводит предел выражения, содержащего обратные тригонометрические функции. Сделаем замену переменных. Возьмем за новую переменную arcsin(x-1), тогда мы получим выражение подобное первому замечательному пределу: (y=arcsin(x-1)).
Заметим, что при ![]() то есть
то есть ![]() ,
,
![]()
12. Найдем 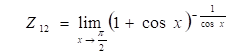 .
.
Здесь имеет место неопределенность типа {1¥}
При раскрытии неопределенностей такого вида пользуются вторым замечательным пределом.
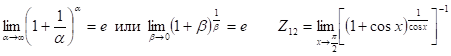
Т. к. при ![]() То положим
То положим ![]()
Обратимся теперь подробнее к вопросу о непрерывности функций.
Вопросы для самоконтроля:
1. Что такое функция? Ее область определения и область значений.
2. Что такое сложная функция?
3. Дайте определение предела функции в т. х0 слева, справа, вообще определение предела.
4. Какие свойства пределов Вы знаете?
5. Какие бесконечно малые называются бесконечно малыми одного порядка?
6. Какие бесконечно малые называются эквивалентными бесконечно малыми?
| < Предыдущая | Следующая > |
|---|