03. Бесконечно малые функции и бесконечно большие функции

Бесконечно малые функции обладают следующими свойствами:

1) Алгебраическая сумма любого конечного числа бесконечно малых в некоторой точке функций есть функция, бесконечно малая в той же точке.

2) Произведение любого конечного числа бесконечно малых в некоторой точке функций есть функция, бесконечно малая в той же точке.

3) Произведение бесконечно малой в некоторой точке функции на функцию ограниченную есть функция, бесконечно малая в той же точке.

Бесконечно малые в некоторой точке х0 функции a(x) и b(x) называются Бесконечно малыми одного порядка, если Если Называется Бесконечно малой более высокого порядка по сравнегию с Бесконечно малые в некоторой точке функции называются Эквивалентными, если Обозначается

Пример 1. Бесконечно малые являются бесконечно малыми одного порядка, т. к.

Пример 2. является бесконечно малой более высокого порядка, чем при , т. к.

Пример 3. Бесконечно малые при являются эквивалентными, так как

Предел отношения бесконечно малых (бесконечно больших) функций не изменится, если каждую из них заменить эквивалентной ей функцией, т. е. Если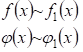

< Предыдущая		Следующая >