02. Пределы, пределы слева, пределы справа
Пределом функции f(х) в точке х0 называется число L такое, что для любого числа e >0 существует число, δ>0 (зависщее от e), что для всех х, принадлежащих Е, удовлетворяющих неравенству 0< │х-х0│< δ, справедливо равенство │f(x)-L│<e.
Предел L обозначается по-разному:
![]() или
или ![]() или
или ![]()
Пределом слева (или справа) функции f(х) в точке х0 называется число L такое, что для любого числа e >0 существуе такое число ![]() >0 (зависящее от e), что для всех х, принадлежащих Е, удовлетворяющих неравенству
>0 (зависящее от e), что для всех х, принадлежащих Е, удовлетворяющих неравенству ![]() (или
(или ![]() ), справедливо неравенство
), справедливо неравенство ![]()
Предел слева обозначается ![]() , а предел справа
, а предел справа ![]()
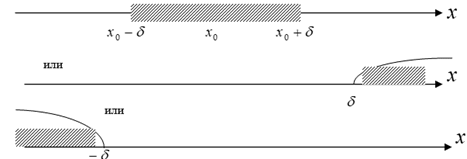
Геометрический смысл предела ![]() функции в точке х0 таков: если значения аргумента Х будут взяты в
функции в точке х0 таков: если значения аргумента Х будут взяты в
D - окрестности точки х0, то соответствующие значения функции останутся в e - окрестности точки L:
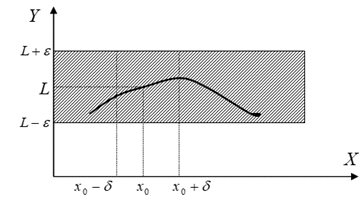
Аналогично, геометрический смысл предела слева ясен из рисунка. Отличие от предыдущего случая состоит в том, что значения аргумента берутся из d - окрестности х0 только слева:
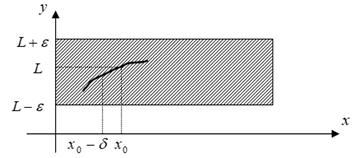
Или для предела справа – значение аргумента берутся из d - окрестности точки х0 только справа от этой точки:
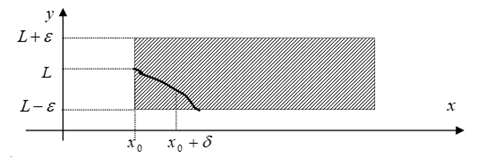
Пределы ![]() и
и ![]() называются Односторонними пределами.
называются Односторонними пределами.
Если оба односторонних предела в точке х0 существуют и равны между собой, то говорят, что функция имеет двухсторонний предел при x®x0 или просто имеет предел при Х стремящимся к х0.
Покажем теперь, что если функция имеет предел, то он единственный. Это легко установить геометрически. Допустим обратное: что существует два предела L1 и L2.
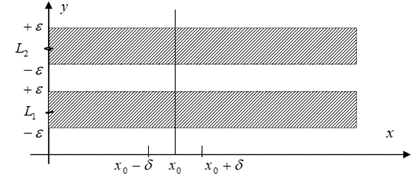
Для любого ε , в соответствии с определением предела можно указать такую d окрестность точки х0, что все значения функции будут находиться в e- окрестности L. Возьмем e столь малым, чтобы обе полосы не имели общих точек. Тогда при х из d окрестности х0 график функции должен находиться одновременно в ε-окрестности L1 ε в ε окрестности L2. Но так как мы рассматриваем только однозначные функции, то график функции не может находиться одновременно в каждой из этих полос. Таким образом, любая функция либо совсем не имеет предела, либо имеет только один.
В случае, если надо дать определение предела при x®+¥ либо x®-¥ , можно дать следующее определение d окрестности точки х0, которое позволит включить в определение предела эти случаи.
Пусть ![]() -
- ![]() - окрестность точки х0, причем
- окрестность точки х0, причем ![]() >0.
>0.
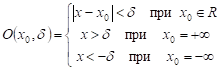
Если ![]() , то функция
, то функция ![]() называется Бесконечно малой в точке
называется Бесконечно малой в точке ![]() . Например, функция
. Например, функция
![]()
Если ![]() То функция называется Бесконечно большой в точке
То функция называется Бесконечно большой в точке ![]() . Например, функция
. Например, функция
![]()
| < Предыдущая | Следующая > |
|---|