18. Переход к нехудшему опорному плану (третий пункт алгоритма)

Улучшим план перевозок за счет загрузки свободной клетки с отрицательной оценкой, для этого для наиболее перспективной свободной клетки строится замкнутый цикл с вершинами в загруженных клетках. Вершинам этого цикла условно присваиваются знаки: свободной клетке – плюс, следующей, по часовой или против часовой стрелке, занятой клетке – минус, следующей – снова плюс и т. д. Из поставок в клетках цикла с «отрицательными» вершинами выбирается наименьшее количество груза, которое и перемещается по клеткам этого цикла: прибавляется к поставкам в «положительных» вершинах и вычитается из поставок в «отрицательных» вершинах, в результате чего баланс цикла не нарушится.

Цикл пересчета

В общем случае цикл пересчета представляет собой замкнутую ломаную линию, состоящую из звеньев, пересекающихся под прямым углом. Каждое звено соединяет две клетки строки (столбца). Цикл включает одну свободную клетку, остальные клетки цикла заняты. В цикле всегда четное число клеток. Для свободной клетки всегда можно построить единственный цикл.

Если из занятых клеток образуется цикл, то план перевозок не является опорным. Цикл строится лишь для свободной клетки.

Например, Найдем оценки свободных клеток начального опорного плана, построенного в последнем примере методом минимального элемента. Используя найденные выше потенциалы строк и столбцов , рассчитаем оценки свободных клеток:

Так как оценка , то найденный план не оптимален. Его можно улучшить путем загрузки этой клетки.

Составим цикл пересчета относительно клетки () (см. таблицу 19).

Из клеток, помеченных знаком «–», выбираем наименьшее количество груза . Прибавляем значение к поставкам в клетках, помеченных знаком «+», и вычитаем из поставок в клетках, помеченных знаком «–». Получим следующий план перевозок (см. таблицу 20).

Таблица 19

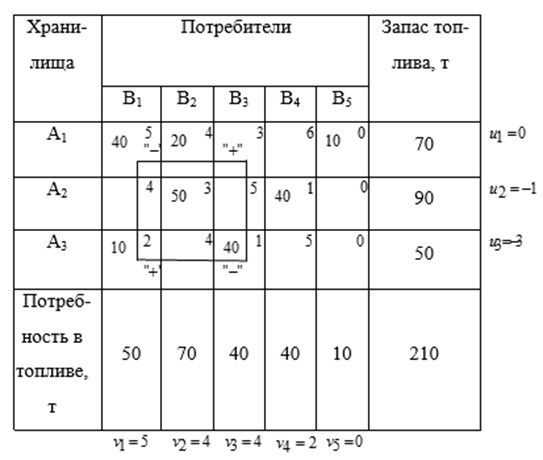
Полученный опорный план является вырожденным, так как число заполненных клеток равно 6 < M + N – 1 = 7. Для преодоления вырожденности плана поставим ноль в любую пустую клетку, не образующую цикла с уже заполненными клетками, например в клетку () (см. таблицу 20).

Таблица 20

Хранилища	Потребители	Запас топлива, т
	В1	В2	В3	В4	В5
А1						70
А2						90
А3						50
Потребность в топливе, т	50	70	40	40	10	210

Проверим найденный план на оптимальность, для этого найдем потенциалы строк и столбцов из решения системы:

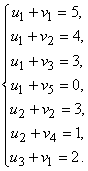
Присвоив , найдем

Запишем потенциалы в последнюю таблицу.

Определим оценки свободных клеток:

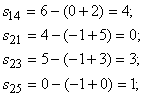
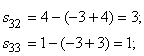
Так как все оценки неотрицательны, то найденный опорный план является оптимальным, а так как имеется нулевая оценка (), то этот план не единственен.

Итак, получили оптимальный план

.

Транспортные издержки для этого плана:

(усл ден. ед.).

Итак, по оптимальному плану необходимо из хранилища А1 потребителю B2 доставить 20 т топлива, потребителю B3  – 40 т топлива; из хранилища А2 потребителю В2 доставить 50 т топлива, а потребителю В4 –40 т топлива; из хранилища А3 доставить 50 т топлива потребителю В1.

При этом затраты на транспортировку будут минимальными и составят 490 усл. ден. ед. Нераспределенное топливо в размере 10 т останется в хранилище А1.

< Предыдущая		Следующая >