19. Динамическое программирование

Динамическое программирование (ДП) – это метод нахождения оптимальных решений в задачах с многошаговой (многоэтапной) структурой.

Приведем общую постановку задачи ДП. Рассматривается управляемый процесс (распределение средств между предприятиями, использование ресурсов в течение ряда лет и т. п.). В результате управления система (объект управления) переводится из начального состояния в состояние . Предположим, что управление можно разбить на шагов. На каждом шаге выбирается одно из множества допустимых управлений , переводящее систему в одно из состояний множества . Элементы множества и определяются из условий конкретной задачи. Последовательность состояний системы можно изобразить в виде графа состояний, представленного на рисунке 2.

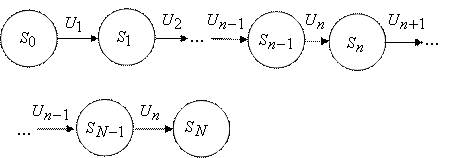Рисунок 2 – Граф состояний

На каждом шаге N достигается эффект . Предположим, что общий эффект является суммой эффектов, достигнутых на каждом шаге. Тогда задача ДП формулируется так: определить допустимое управление , переводящее систему из состояния в состояние , при котором функция цели принимает наибольшее (наименьшее) значение, т. е.

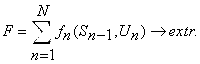
Решение задач методом ДП осуществляется на основе принципа оптимальности, который был сформулирован американским ученым

Р. Беллманом: каково бы ни было состояние системы в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный.

Обозначим через условно-оптимальное значение целевой функции на интервале от шага N до последнего -го шага включительно при условии, что перед N-ым шагом система находилась в одном из состояний множества , а на N-ом шаге было выбрано такое управление из множества , которое обеспечило целевой функции условно-оптимальное значение, тогда условно-оптимальное значение целевой функции в интервале от (N+1)-го до -го шага включительно.

В принятых обозначениях принцип оптимальности Беллмана можно записать в математической форме следующим образом:

, (4.1)

Равенство (4.1) называется основным функциональным уравнением динамического программирования. Для каждой конкретной задачи уравнение имеет особый вид.

Вычислительная процедура метода ДП распадается на два этапа: условную и безусловную оптимизацию.

На этапе Условной оптимизации в соответствии с функциональным уравнением определяются оптимальные управления для всех возможных состояний на каждом шаге, начиная с последнего.

На этапе Безусловной Оптимизации шаги рассматриваются, начиная с первого. Поскольку исходное состояние известно, выбирается оптимальное управление из множества . Выбранное оптимальное управление приводит систему в вполне определенное состояние . Благодаря тому, что исходное состояние в начале второго шага известно, становится возможным выбрать оптимальное управление на втором шаге и т. д. Таким образом, строится цепь взаимосвязанных решений безусловной оптимизации.

Рассмотрим интерпретацию приведенного выше итерационного процесса на следующем примере.

Пример 9 Задача оптимального распределения капиталовложений

Для увеличения объемов выпуска пользующейся повышенным спросом продукции трем предприятиям выделены капиталовложения в размере 700 млн. руб. Каждому из предприятий может быть выделено капиталовложений в размере 0, 100, 200, 300, 400, 500, 600, 700 млн. руб. При этом прирост выпуска продукции каждым из предприятий в зависимости от капиталовложений известно и приведено в таблице 21.

Таблица 21

Объем капиталовложений (млн. руб.)	Прирост выпуска продукции (млн. руб.) в зависимости от объема капиталовложений
Предприятие 1	Предприятие 2	Предприятие 3
0	0	0	0
100	30	50	40
200	50	80	50
300	90	90	110
400	110	150	120
500	170	190	180
600	180	210	220
700	210	220	240

Найти распределение капиталовложений между предприятиями, обеспечивающее максимальное увеличение выпуска продукции.

Решение

Сначала поставленную задачу нужно рассмотреть как многошаговую. Будем рассматривать эффективность вложения средств на одном (например, первом предприятии), на двух предприятиях (первое и второе) и, наконец, на трех предприятиях вместе. Если млн. руб. – это капиталовложения в J-ое предприятие (J = 1,2,3), то задача состоит в определении наибольшего значения функции при условии .

Рекуррентное соотношение Беллмана в нашем случае приводит к следующим функциональным уравнениям:

Здесь функция определяет максимальный прирост выпуска продукции при выделении X млн. рублей капиталовложений первому предприятию. определяет максимальный выпуск продукции при распределении X млн. рублей между первым и вторым предприятиями. – максимальный прирост при выделении всем трем предприятиям млн. рублей.

I этап. Условная оптимизация

1-й шаг. Находим по формуле (4.2).

Пусть , тогда .

При ,

Результаты вычислений и полученные соответствующие условно оптимальные значения Запишем в виде таблицы 22.

Таблица 22

Объем капиталовложений X, выделяемых первому предприятию, млн. руб.	Максимальный прирост выпуска продукции, млн. руб.	Условно оптимальный объем капиталовложений , выделяемый первому предприятию, млн. руб.
0	0	0
100	30	100
200	50	200
300	90	300
400	110	400
500	170	500
600	180	600
700	210	700

2-й шаг. Используя полученную таблицу, определим условно оптимальные объемы капиталовложений, выделенных второму предприятию. Для этого находим по формуле (4.3).

Пусть , тогда

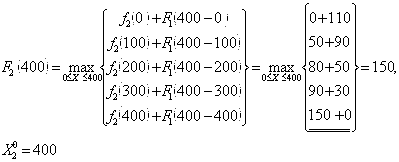
При ,

При

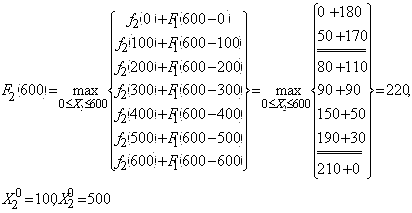
При ,

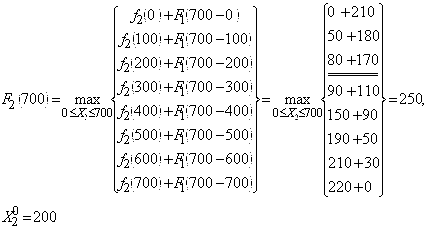Полученные результаты и найденные условно оптимальные объемы капиталовложений второму предприятию записываем в виде таблицы 23.

Таблица 23

Объем капиталовложений X, выделенных двум предприятиям, млн. руб.	Максимальный прирост выпуска продукции первым и вторым предприятиями вместе, млн. руб.	Условно оптимальный объем капиталовложений , выделяемых второму предприятию, Млн. руб.
0	0	0
100	50	100
200	80	100,200
300	110	200
400	150	400
500	190	500
600	220	100,500
700	250	200

3-й шаг. Переходим к нахождению значений по формуле (4.4).

Так как теперь предприятий три, то им будет выделен весь объем капиталовложений, т. е. X = 700.

II этап. Безусловная оптимизация

Определяем компоненты оптимальной стратегии.

1-й шаг. Итак, максимальный прирост выпуска продукции составит 270 млн. руб. При этом третьему предприятию нужно выделить = 600 млн. руб.

2-й шаг. Тогда и по таблице 23 находим, что максимальный прирост выпуска продукции при распределении 100 млн. руб. будет при , следовательно, второму предприятию нужно выделить = 100 млн. руб.

3-й шаг. Так как , то . Значит, первому предприятию нужно выделить = 0 млн. руб.

Итак, оптимальный план распределения капиталовложений между предприятиями обеспечит максимальное увеличение выпуска продукции в размере Млн. руб. или в качестве проверки

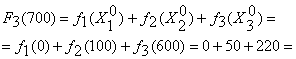
= 270 (млн. руб.)

< Предыдущая		Следующая >