17. Проверка на оптимальность невырожденного опорного плана методом потенциалов (второй пункт алгоритма)

1 Каждому поставщику поставим в соответствие потенциал , а каждому потребителю потенциал .

Тогда каждой занятой клетке будет соответствовать уравнение

.

Так как всех занятых клеток должно быть M + N – 1, т. е. на единицу меньше числа потенциалов, то для нахождения необходимо решить систему из M + N – 1 уравнений с M + N неизвестными. Система является линейно-зависимой и, чтобы найти частное решение, одному из потенциалов нужно придать произвольное числовое значение, тогда остальные потенциалы определяются однозначно. Например, потенциалы строк и столбцов для начального опорного плана, найденного в последнем примере методом минимального элемента определим из решения системы

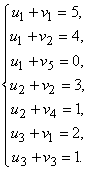
Система является линейно-зависимой, для нахождения одного из частных решений придадим одному из потенциалов числовое значение, например , тогда

2 Для исследования плана на оптимальность для каждой свободной клетки считаем оценки по формуле

;

А) если все оценки положительны, то найденный опорный план оптимален и единственен ;

Б) если наряду с положительными оценками встречаются и нулевые оценки , то найденный опорный план оптимален, но не единственен;

В) если оценка хотя бы одной свободной клетки отрицательна , то опорный план не является оптимальным, его можно улучшить за счет загрузки этой клетки. Если таких клеток несколько, то наиболее перспективной для загрузки является клетка с наименьшей оценкой. Например, для клеток имеем оценки . Здесь наиболее потенциальной (перспективной для загрузки) является клетка .

< Предыдущая		Следующая >