34. Дивергенция векторного поля
Интегральные характеристики – поток и линейный интеграл – характеризуют векторное поле “в целом”. Количественную характеристику поля в каждой точке дают, вводимые ниже, дифференциальные характеристики. Введем понятие дивергенции.
Окружим произвольную точку M поверхностью (S) произвольной формы (например, сферой достаточно малого радиуса). Пусть (V) – объем, заключенный внутри поверхности (S).
Определение. Конечный предел отношения потока поля через поверхность (S) к объему, заключенному внутри нее при стягивании поверхности к точке M и стремлении объема V к нулю называется дивергенцией векторного поля ![]() в точке M:
в точке M:
 (1.10¢)
(1.10¢)
Замечание. Определение (1.10) есть инвариантное (не зависящее от системы координат) определение дивергенции.
Дивергенция характеризует отнесенную к единице объема мощность потока векторного поля, “исходящего” из точки M, то есть мощность источника (при ![]() ), или стока (при
), или стока (при ![]() ), находящегося в точке M.
), находящегося в точке M.
В декартовой системе координат дивергенция вычисляется по формуле
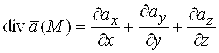 . (1.10)
. (1.10)
Свойства дивергенции. Пусть ![]() И
И ![]() - векторные поля,
- векторные поля, ![]() - скалярная функция. Тогда:
- скалярная функция. Тогда:
1) ![]() ; 2)
; 2) ![]() . (1.11)
. (1.11)
С учетом формулы (1.10) перепишем формулу Гаусса-Остроградского (1.6)
![]() (1.12)
(1.12)
- поток векторного поля ![]() через замкнутую поверхность (S) равен тройному интегралу по объему (V), заключенному внутри этой поверхности от дивергенции поля.
через замкнутую поверхность (S) равен тройному интегралу по объему (V), заключенному внутри этой поверхности от дивергенции поля.
Пример 1. Вычислить ![]() .
.
Решение. 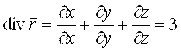 .
.
Пример 2. Вычислить ![]() , где U(M) – скалярная функция,
, где U(M) – скалярная функция, ![]()
![]() - векторная функция.
- векторная функция.
Решение. По формуле (1.10) находим: 
![]()


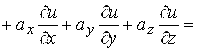
![]() .
.
Пример 3. Используя теорему Гаусса-Остроградского (1.12), найти поток векторного поля ![]() через всю поверхность (S) тела (V):
через всю поверхность (S) тела (V):
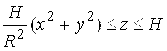 в направлении внешней нормали.
в направлении внешней нормали.
Решение. Имеем ![]() . Поэтому
. Поэтому ![]() =
=![]() . Для вычисления тройного интеграла перейдем к цилиндрическим координатам. Уравнение поверхности примет вид
. Для вычисления тройного интеграла перейдем к цилиндрическим координатам. Уравнение поверхности примет вид ![]() ,
, ![]()

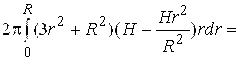 =
=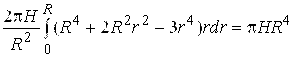 .
.
| < Предыдущая | Следующая > |
|---|